河南省南阳市淅川县2018-2019学年七年级上学期数学期中考试试卷

试卷更新日期：2019-10-09 类型：期中考试

进入出卷网下载

一、单选题

1. ﹣ $\frac{2}{3}$ 的相反数是（）

A、 $\frac{3}{2}$ B、 $\frac{2}{3}$ C、﹣ $\frac{2}{3}$ D、﹣ $\frac{3}{2}$

查看试题解析
2. 大于﹣1且不大于3的整数共有（）

A、3 B、4 C、5 D、6

查看试题解析
3. 若 $a^{2} = 1$ ，b是2的相反数，则a+b的值为（）

A、﹣3 B、﹣1 C、﹣1或﹣3 D、1或﹣3

查看试题解析
4. 某年全国财政收入为9057.97亿元，9057.97用科学记数法表示为（）

A、9.05797×10² B、9.05797×10³ C、9.05797×10⁴ D、9.05797×10⁵

查看试题解析
5. 下列各式中，计算结果等于0的是（）

A、(－2)²－(－2²) B、－2²－2² C、－2²＋(－2)² D、－2²－(－2)²

查看试题解析
6. 下列表述中，正确的是（）

A、有理数有最大的数，也有最小的数 B、有理数有最大的数，但没有最小的数 C、有理数有最小的数，但没有最大的数 D、有理数既没有最大的数，也没有最小的数

查看试题解析
7. 某件商品原价18元，后来又跌1.5元，下午又涨价0.3元，则这一商品最终价格是（）

A、0.3元 B、16.2元 C、16.8元 D、18元

查看试题解析
8. 身份证号码告诉我们很多信息，某人的身份证号码是610323196209232913，其中，61、03、23是此人所属的省（市、自治区）、市、县（市、区）的编码，1962、09、23是此人出生的年、月、日，291是顺序码，3为校验码，那么身份证号码41292719721124691x的人的生日是（）

A、7月21日 B、2月4日 C、11月24日 D、12月4

查看试题解析
9. a，b，c在数轴上的对应点的位置如图所示，下列式子：①b＋c＞0；②a＋b＞a＋c；③bc＞ac；④ab＞ac.其中正确的有（）

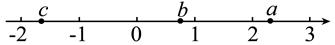A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，图中“ $⊙$ ”是按一定的规律排列，根据此规律，有2019个“ $⊙$ ”图案的是（）

A、第689个图 B、第688个图 C、第678个图 D、第673个图

查看试题解析

二、填空题

11. 计算（﹣1）÷6×（﹣ $\frac{1}{6}$ ）=.

查看试题解析
12. 定义a※b=ab﹣2b，（1※2）※3=.

查看试题解析
13. 已知|x|=3，|y|=2，且x+y＞0，则xy=.

查看试题解析
14. 已知m²﹣2n﹣1=0，则2m²﹣4n+5=.

查看试题解析
15. 有一列数a₁ ， a₂ ， a₃ ， …，a_n ，已知a₁=1，a₂=2，从第三个数开始，每个数都等于它前面的两个数中第二个数除以第一个数所得的商，例a₃=a₂÷a₁=2……，那么a₂₀₁₈=.

查看试题解析

三、解答题

16. 计算

(1)、﹣8.125+7 $\frac{1}{8}$ ﹣4 $\frac{3}{4}$ + $\frac{3}{4}$

(2)、（﹣2）²﹣2²﹣|﹣ $\frac{1}{4}$ |×（﹣10）²

查看试题解析
17. 计算

(1)、﹣1⁴+（1﹣0.5）× $\frac{1}{3}$ ×[2﹣（﹣3）²]

(2)、[2 $\frac{1}{2}$ +（ $\frac{3}{8}$ + $\frac{1}{6}$ ﹣ $\frac{3}{4}$ ）×24]÷（﹣5）×（﹣1）²⁰¹⁸

查看试题解析
18. 数轴是一个非常重要的数学工具，通过它把数和数轴上的点建立起对应关系，揭示了数与点之间的内在的联系，它是“数形结合”的基础，请利用数轴解决下列问题：

(1)、画出数轴，并在数轴上画出表示下列各数的点：﹣4.5，﹣2，0，1.5，3；

(2)、用“＞”号将（1）中各数连接起来；

(3)、直接填空：数轴上表示3和表示1的两点之间的距离是，数轴上若A点表示的数为4，B点表示的数为﹣2，则A、B之间的距离是.

(4)、若数轴上A点表示的数为﹣3，且A、B两点间的距离为3，则B点表示的数为.

查看试题解析
19. 已知：a，b互为相反数，c，d互为倒数，x的绝对值是2，求：（a+b+cd）x+（a+b）²⁰¹⁷+（﹣cd）²⁰¹⁸的值.

查看试题解析
20. 阅读第①小题的计算方法，再计算第②小题.
①–5 $\frac{5}{6}$ +（–9 $\frac{2}{3}$ ）+17 $\frac{3}{4}$ +（–3 $\frac{1}{2}$ ）.

解：原式=[（–5）+（– $\frac{5}{6}$ ）]+[（–9）+（– $\frac{2}{3}$ ）]+（17+ $\frac{3}{4}$ ）+[（–3+（– $\frac{1}{2}$ ）]

=[（–5）+（–9）+（–3）+17]+[（– $\frac{5}{6}$ ）+（– $\frac{2}{3}$ ）+（– $\frac{1}{2}$ ）+ $\frac{3}{4}$ ]

=0+（–1 $\frac{1}{4}$ ）

=–1 $\frac{1}{4}$ .

上述这种方法叫做拆项法.灵活运用加法的交换律、结合律可使运算简便.

②仿照上面的方法计算：（–2017 $\frac{2}{3}$ ）+（–2018 $\frac{5}{6}$ ）+4034+（– $\frac{1}{2}$ ）.

查看试题解析
21.

(1)、分别求出代数式a²﹣2ab+b²和（a﹣b）²的值.
①其中a= $\frac{1}{2}$ ，b=3；②a=5，b=3；③a=﹣1，b=2.

(2)、观察（1）中的①②③你发现这两个多项式有什么关系，直接写出.

(3)、利用你发现的规律，求出1.437²﹣2×1.437×0.437+0.437²的值.

查看试题解析

22. 某中学七年级四班的同学在体检中测量了自己的身高，并求出了该班同学的平均身高.

(1)、下表给出了该班5名同学的身高情况（单位：cm），试完成该表，并求出该班同学的平均身高.

姓名

刘杰

刘涛

李明

张春

刘建

身高

161

165

155

身高与全班同

学平均身高差

﹣1

(2)、谁最高？谁最矮？

(3)、计算这5名同学的平均身高是多少？

查看试题解析

23. “十一”期间，小华约同学一起开车到距家100千米的景点旅游，出发前，汽车油箱内储油35升，当行驶80千米时，发现油箱余油量为25升（假设行驶过程中汽车的耗油量是均匀的）.

(1)、求该车平均每千米的耗油量，并写出行驶路程x（千米）与剩余油量Q（升）的关系式；

(2)、当x=60（千米）时，求剩余油量Q的值；

(3)、当油箱中剩余油量低于3升时，汽车将自动报警，如果往返途中不加油，他们能否在汽车报警前回到家？请说明理由.

查看试题解析