河南省洛阳市伊川县2019-2020学年九年级上学期数学第一次月考试卷

试卷更新日期：2019-10-09 类型：月考试卷

进入出卷网下载

一、单选题

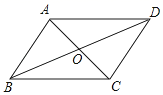
1. 如图，在四边形ABCD中，对角线AC，BD相交于点O，AO=CO，BO=DO．添加下列条件，不能判定四边形ABCD是菱形的是（）

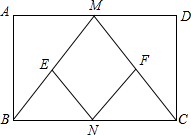
A、AB=AD B、AC=BD C、AC⊥BD D、∠ABO=∠CBO

查看试题解析
2. 下列方程中是关于x的一元二次方程的是（）

A、 $x^{2} + \frac{1}{x^{2}} = 0$ B、 $a x^{2} + b x + c = 0$ C、 $(x - 1) (x - 2) = 0$ D、 $3 x^{2} - 2 x y - 5 y^{2} = 0$

查看试题解析
3. 已知三角形两边长分别为2和9，第三边的长为方程 $x^{2} - 14 x + 48 = 0$ 的一根，则这个三角形的周长为（）

A、11 B、17 C、17或19 D、19

查看试题解析
4. 如图，过矩形 $A B C D$ 的对角线 $A C$ 的中点 $O$ 作 $E F ⊥ A C$ ，交 $B C$ 边于点 $E$ ，交 $A D$ 边于点 $F$ ，分别连接 $A E$ 、 $C F$ .若 $A B = \sqrt{3}$ ， $∠ D C F = 30 °$ ，则 $E F$ 的长为（）

A、 $2$ B、 $3$ C、 $\frac{\sqrt{3}}{2}$ D、 $\sqrt{3}$

查看试题解析
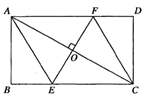5.
如图，四边形ABCD中，对角线相交于点O，E、F、G、H分别是AD、BD、BC、AC的中点，要使四边形EFGH是菱形，则四边形ABCD需满足的条件是（　　）

A、AB=AD B、AC=BD C、AD=BC D、AB=CD

查看试题解析
6. 如图，菱形纸片ABCD中，∠A＝60°，折叠菱形纸片ABCD，使点C落在DP(P为AB中点)所在的直线上，得到经过点D的折痕DE，则∠DEC的大小为（）

A、78° B、45° C、60° D、75°

查看试题解析
7. 要组织一次排球邀请赛，参赛的每个队之间都要比赛一场，根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛.设比赛组织者应邀请x个队参赛，则x满足的关系式为（）

A、 $\frac{1}{2}$ x（x+1）＝28 B、 $\frac{1}{2}$ x（x﹣1）＝28 C、x（x+1）＝28 D、x（x﹣1）＝28

查看试题解析
8. 在一个不透明的布袋中，有黄色、白色的玻璃球共有10个，除颜色外，形状、大小、质地等完全相同.小刚通过多次摸球试验后发现摸到黄色球的频率稳定在40%，则布袋中白色球的个数很可能是（）

A、4个 B、5个 C、6个 D、7个

查看试题解析
9. 如图所示，在Rt△ABC中，∠C=90°，AC=11cm，点P从点A出发沿AC以1cm/s的速度移动，点Q从点C出发沿CB以2cm/s的速度移动，如果P，Q分别从A，C两点同时出发，当它们相距10cm时所需的时间为（）

A、3s B、4s C、5s D、3s或1.4s

查看试题解析
10. 一元二次方程 $\sqrt{2} x^{2} - 2 \sqrt{3} x + \sqrt{5} = 0$ 的根的情况是（）

A、方程没有实数根 B、方程有两个相等的实数根 C、方程有两个不相等的实数根 D、无法判断方程实数根情况

查看试题解析

二、填空题

11. 某药品原价每盒25元，为了响应国家解决老百姓看病贵的号召，经过连续两次降价，现在售价每盒16元，则该药品平均每次降价的百分率是．

查看试题解析
12. 如图，在正方形ABCD中，对角线AC与BD相交于点O，E为BC上一点，CE＝5，F为DE的中点.若△CEF的周长为18，则OF的长为.

查看试题解析
13. 某种文化衫，平均每天销售40件，每件盈利20元，若每件降价1元，则每天可多售10件，如果每天要盈利1080元，每件应降价元.

查看试题解析
14. 如图，E为正方形ABCD边BC延长线上一点，且CE=BD，AE交DC于F，则∠AFC=.

查看试题解析
15. 如图，正方形ABCD的面积为8cm² ，且其对角线相交于点O，点O是正方形A′B′C′O的一个顶点，如果两个正方形的边长相等，那么正方形A′B′C′O绕点O无论怎样转动，两个正方形重叠部分的面积为cm².

查看试题解析

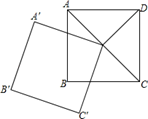
三、解答题

16. 解下列一元二次方程：

(1)、-x²+4x-3=0(配方法）

(2)、 $x^{2} - 4 x - 2 = 0$ ；

(3)、 $3 x^{2} - 8 x + 4 = 0$ ；

(4)、3x(x-1)=2-2x.

查看试题解析
17. 已知关于x的一元二次方程x²+2（k﹣1）x+k²﹣1=0有两个不相等的实数根．

(1)、求实数k的取值范围；

(2)、0可能是方程的一个根吗？若是，请求出它的另一个根；若不是，请说明理由．

查看试题解析
18. 有两个同学做了一个数字游戏：有三张正面写有数字-1，0，1的卡片片它们背面完全相同，将这三张卡片背面朝上洗匀后，其中一个同学随机抽取一张，将其正面的数字作为p的值，然后将卡片放回洗匀，另一个同学再从这三张卡片中随机抽取一张，将其正面的数字作为q的值，两次结果记为（p，q）

(1)、请用树状图或列表法表示（p，q）所有可能出现的结果；

(2)、求满足关于x的方程x²+px+q=0没有实数根的概率。

查看试题解析
19. 已知：如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，

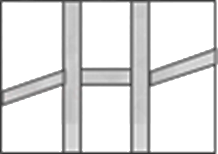
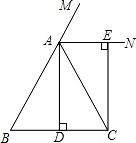(1)、求证：四边形ADCE为矩形；

(2)、当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明.

查看试题解析
20. 为响应市委市政府提出的建设“绿色襄阳”的号召，我市某单位准备将院内一块长30m，宽20m的长方形空地，建成一个矩形花园.要求在花园中修两条纵向平行和一条横向弯折的小道，剩余的地方种植花草，如图所示，要使种植花草的面积为532m² ，那么小道进出口的宽度应为多少米？（注：所有小道进出口的宽度相等，且每段小道均为平行四边形）

查看试题解析
21. 如图，已知：在四边形ABFC中，∠ACB=90°，BC的垂直平分线EF交BC于点D，交AB于点E，且CF=AE；

(1)、试判断四边形BECF是什么四边形？并说明理由.

(2)、当∠A的大小满足什么条件时，四边形BECF是正方形？请回答并证明你的结论.

查看试题解析
22. 已知：如图，在矩形ABCD中，M、N分别是边AD、BC的中点，E、F分别是线段BM、CM的中点

(1)、求证：△ABM≌△DCM

(2)、判断四边形MENF是什么特殊四边形，并证明你的结论；

(3)、当AD：AB=_时，四边形MENF是正方形（只写结论，不需证明）

查看试题解析