浙江省义乌市六校2019-2020学年八年级上学期数学第一次月考试卷
试卷更新日期:2019-10-09 类型:月考试卷
一、选择题(本题有10小题,每小题4分,共40分)
-
1. 若有两条线段长分别为3cm和4cm,则下列长度的线段能与其组成三角形的是( )A、1cm B、5cm C、7cm D、9cm2. 工人师傅砌门时,常用一根木条固定长方形门框,使其不变形,这样做的根据是( )A、两点之间的线段最短 B、三角形具有稳定性 C、长方形是轴对称图形 D、长方形的四个角都是直角3. 画△ABC中AB边上的高,下列画法中正确的是( )A、
 B、
B、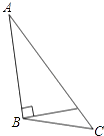 C、
C、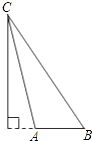 D、
D、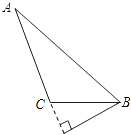 4. 下列各数中,可以用来说明命题“任何偶数都是4的倍数”是假命题的反例是( )A、5 B、2 C、4 D、85. 下面各条件中,能使△ABC≌△DEF的条件是( )A、AB=DE,∠A=∠D,BC=EF B、AB=BC,∠B=∠E,DE=EF C、AB=EF,∠A=∠D,AC=DF D、BC=EF,∠C=∠F,AC=DF6. 如图在△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法正确的个数是( )
4. 下列各数中,可以用来说明命题“任何偶数都是4的倍数”是假命题的反例是( )A、5 B、2 C、4 D、85. 下面各条件中,能使△ABC≌△DEF的条件是( )A、AB=DE,∠A=∠D,BC=EF B、AB=BC,∠B=∠E,DE=EF C、AB=EF,∠A=∠D,AC=DF D、BC=EF,∠C=∠F,AC=DF6. 如图在△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法正确的个数是( )( 1 )AD平分∠EDF;(2)△EBD≌△FCD;(3)BD=CD;(4)AD⊥BC.
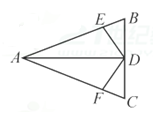 A、1个 B、2个 C、3个 D、4个7. 如图是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A、1个 B、2个 C、3个 D、4个7. 如图是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )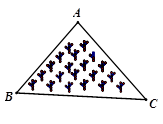 A、△ABC 的三条中线的交点 B、△ABC 三边的中垂线的交点 C、△ABC 三条角平分线的交点 D、△ABC 三条高所在直线的交点8. 如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )
A、△ABC 的三条中线的交点 B、△ABC 三边的中垂线的交点 C、△ABC 三条角平分线的交点 D、△ABC 三条高所在直线的交点8. 如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )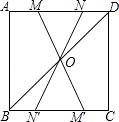 A、2对 B、3对 C、4对 D、5对9. 某校八年级四个班的代表队准备举行篮球赛.甲、乙、丙三位同学预测比赛的结果如下:甲说:“802班得冠军,804班得第三”;乙说:“801班得第四,803班得亚军”;丙说:“803班得第三,804班得冠军”赛后得知,三人都只猜对了一半,则得冠军的是( )A、801班 B、802班 C、803班 D、804班10. 如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列三个结论:
A、2对 B、3对 C、4对 D、5对9. 某校八年级四个班的代表队准备举行篮球赛.甲、乙、丙三位同学预测比赛的结果如下:甲说:“802班得冠军,804班得第三”;乙说:“801班得第四,803班得亚军”;丙说:“803班得第三,804班得冠军”赛后得知,三人都只猜对了一半,则得冠军的是( )A、801班 B、802班 C、803班 D、804班10. 如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列三个结论: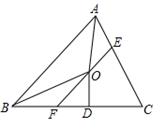
①∠AOB=90°+
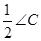 ②当∠C=90°时,E,F分别是AC,BC的中点;③若OD=a,CE+CF=2b,则S△CEF=ab其中正确的是( )A、①②③ B、①③ C、①② D、①
②当∠C=90°时,E,F分别是AC,BC的中点;③若OD=a,CE+CF=2b,则S△CEF=ab其中正确的是( )A、①②③ B、①③ C、①② D、①二、填空题(本题有6小题,每小题5分,共30分)
-
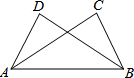
11. 把命题“同角的余角相等”改写成“如果…,那么…”的形式是。12. 如图点C,D在AB同侧,AD=BC,添加一个条件就能使△ABD≌△BAC。
 13. 如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A'处,折痕为CD,则∠A'DB=度。
13. 如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A'处,折痕为CD,则∠A'DB=度。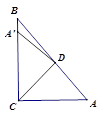 14. 如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且△ABC的面积等于4cm2 , 则阴影部分图形面积等于cm2
14. 如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且△ABC的面积等于4cm2 , 则阴影部分图形面积等于cm2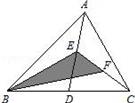 15. 如图AD是△ABC的中线,AB=7,AC=5,AD=x,则x的取值范围是。
15. 如图AD是△ABC的中线,AB=7,AC=5,AD=x,则x的取值范围是。 16. 已知AD,AE分别是△ABC的高线和角平分线。(1)、若∠B=70°,∠C=30°,则∠DAE=度。(2)、若∠B=x°,∠C=y°,则∠DAE=度(用x,y的代数式表示)。
16. 已知AD,AE分别是△ABC的高线和角平分线。(1)、若∠B=70°,∠C=30°,则∠DAE=度。(2)、若∠B=x°,∠C=y°,则∠DAE=度(用x,y的代数式表示)。三、解答题(17,18,19,20每题8分,21题10分,22,23每题12分,24题14分)
-
17.
已知线段a,b及∠α,用直尺和圆规作△ABC,使∠B=∠α,AB=a,BC=b.
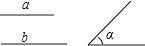 18. 如图,CD是线段AB的垂直平分线,则∠CAD=∠CBD.请说明理由:
18. 如图,CD是线段AB的垂直平分线,则∠CAD=∠CBD.请说明理由: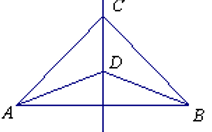
解:∵ CD是线段AB的垂直平分线
∴ AC=BC,AD=DB( )
在△ADC和△BDC中,
 ( )
( )∴△ADC≌和△BDC( ).
∴ ∠CAD=∠CBD( ).
19. 已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,求证:△ABC≌△DEF.
 20. 如图:AB=AC,AD=AE,AB⊥AC,AD⊥AE。
20. 如图:AB=AC,AD=AE,AB⊥AC,AD⊥AE。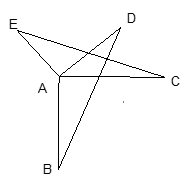 (1)、求证:△EAC≌△DAB(2)、判断线段EC与线段BD的关系,并说明理由21. 已知:如图,AB=AD,BC=DC,E、F分别是DC、BC的中点,
(1)、求证:△EAC≌△DAB(2)、判断线段EC与线段BD的关系,并说明理由21. 已知:如图,AB=AD,BC=DC,E、F分别是DC、BC的中点,求证: AE=AF
 22. 如图,已知在△ABC中,∠ABC与∠ACB的平分线交于点P.
22. 如图,已知在△ABC中,∠ABC与∠ACB的平分线交于点P.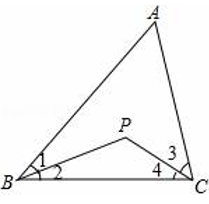 (1)、当∠A=40°,∠ABC=60°时,求∠BPC的度数;(2)、当∠A=α°时,求∠BPC的度数.(用α的代数式表示)
(1)、当∠A=40°,∠ABC=60°时,求∠BPC的度数;(2)、当∠A=α°时,求∠BPC的度数.(用α的代数式表示)
(3)、小明研究时发现:如果延长AB至D,再过点B作BQ⊥BP,那么BQ就是∠CBD的平分线。请你证明小明的结论.
23. 如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段AB上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线AC段于E.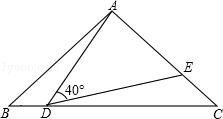 (1)、当∠BDA=115°时,∠BAD=°,∠DEC=°;(2)、当DC等于多少时,△ABD与△DCE全等?请说明理由;(3)、在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.
(1)、当∠BDA=115°时,∠BAD=°,∠DEC=°;(2)、当DC等于多少时,△ABD与△DCE全等?请说明理由;(3)、在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.
24. △ABC是等边三角形,P为平面内的一个动点,BP=BA,0º<∠PBC<180 º,DB平分∠PBC,且DB=DA.
 (1)、当BP与BA重合时(如图1),求∠BPD的度数;(2)、当BP在∠ABC的内部时(如图2),求∠BPD的度数;(3)、当BP在∠ABC的外部时,请你直接写出∠BPD的度数.
(1)、当BP与BA重合时(如图1),求∠BPD的度数;(2)、当BP在∠ABC的内部时(如图2),求∠BPD的度数;(3)、当BP在∠ABC的外部时,请你直接写出∠BPD的度数.