初中数学人教版九年级上学期 第二十四章测试卷
试卷更新日期:2019-10-08 类型:单元试卷
一、单选题
-
1. 已知正方形ABCD的边长为2,点E为正方形所在平面内一点,满足∠AED=90°,连接CE,若点F是CE的中点,则BF的最小值为( )
 A、2 B、 -1 C、 D、22. 如图,四边形 是半圆的内接四边形, 是直径, .若 ,则 的度数等于( )
A、2 B、 -1 C、 D、22. 如图,四边形 是半圆的内接四边形, 是直径, .若 ,则 的度数等于( )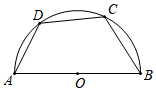 A、 B、 C、 D、3. 如图,AB是⊙O的直径,点C、D在⊙O上,且点C,D在AB的异侧,连结AD,OD,OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )
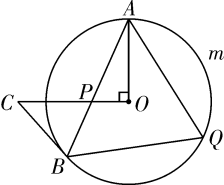
A、 B、 C、 D、3. 如图,AB是⊙O的直径,点C、D在⊙O上,且点C,D在AB的异侧,连结AD,OD,OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )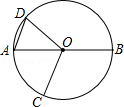 A、70° B、60° C、50° D、40°4. 如图,PA,PB分别与⊙O相切于A,B两点,点C为⊙O上一点,连接AC,BC,若∠P=50°,则∠ACB的度数为( ).
A、70° B、60° C、50° D、40°4. 如图,PA,PB分别与⊙O相切于A,B两点,点C为⊙O上一点,连接AC,BC,若∠P=50°,则∠ACB的度数为( ).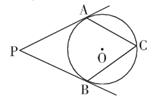 A、60° B、75° C、70° D、65°5. 如图,PA是⊙O的切线,切点为A,PO的延长线交⊙O于点B,若∠P=40°,则∠B的度数为( )
A、60° B、75° C、70° D、65°5. 如图,PA是⊙O的切线,切点为A,PO的延长线交⊙O于点B,若∠P=40°,则∠B的度数为( )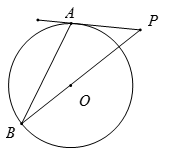 A、20° B、25° C、40° D、50°6. 如图,在正方形 中,点 是对角线 的交点,过点 作射线分别交 于点 ,且 ,交 于点 .给出下列结论: ; C; 四边形 的面积为正方形 面积的 ; .其中正确的是( )
A、20° B、25° C、40° D、50°6. 如图,在正方形 中,点 是对角线 的交点,过点 作射线分别交 于点 ,且 ,交 于点 .给出下列结论: ; C; 四边形 的面积为正方形 面积的 ; .其中正确的是( ) A、 B、 C、 D、7. 如图,已知正五边形 ABCDE内接于⊙O,连结BD,则∠ABD的度数是( )
A、 B、 C、 D、7. 如图,已知正五边形 ABCDE内接于⊙O,连结BD,则∠ABD的度数是( ) A、60° B、70° C、72° D、144°8. 如图,在 中, ,将△AOC绕点O顺时针旋转 后得到 ,则AC边在旋转过程中所扫过的图形的面积为( ) .
A、60° B、70° C、72° D、144°8. 如图,在 中, ,将△AOC绕点O顺时针旋转 后得到 ,则AC边在旋转过程中所扫过的图形的面积为( ) .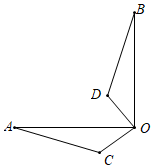 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 用反证法证明“a>b”时,首先应该假设 .
10. 已知一条弧所对的圆周角的度数是15°,则它所对的圆心角的度数是.11. 如图,点A、B、C在⊙O上,BC=6,∠BAC=30°,则⊙O的半径为.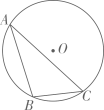 12. 如图,AC是⊙O的内接正六边形的一边,点B在弧AC上,且BC是⊙O的内接正十边形的一边,若AB是⊙O的内接正n边形的一边,则n=。
12. 如图,AC是⊙O的内接正六边形的一边,点B在弧AC上,且BC是⊙O的内接正十边形的一边,若AB是⊙O的内接正n边形的一边,则n=。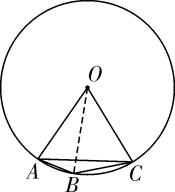 13. 若正六边形的边长为3,则其较长的一条对角线长为.
13. 若正六边形的边长为3,则其较长的一条对角线长为.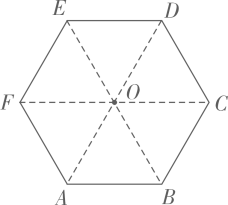 14. 如图,五边形 ABCDE 是⊙O 的内接正五边形, AF 是⊙O 的直径,则∠ BDF 的度数是°
14. 如图,五边形 ABCDE 是⊙O 的内接正五边形, AF 是⊙O 的直径,则∠ BDF 的度数是°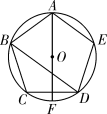 15. 如图,在平面直角坐标系中,已知 经过原点 ,与 轴、 轴分别交于 、 两点,点 坐标为 , 与 交于点 , ,则圆中阴影部分的面积为.
15. 如图,在平面直角坐标系中,已知 经过原点 ,与 轴、 轴分别交于 、 两点,点 坐标为 , 与 交于点 , ,则圆中阴影部分的面积为.
三、作图题
-
16. 如图,在边长均为1的正方形网格纸上有 和 ,顶点A、B,C,D、E、F均在格点上,如果 是由 绕着某点O旋转得到的,点 的对应点是点D,点C的对应点是点 请按要求完成以下操作或运算:
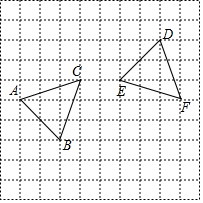 (1)、在图上找到点O的位置 不写作法,但要标出字母 ,并写出点O的坐标;(2)、求点B绕着点O顺时针旋转到点E所经过的路径长.17. 如图,已知在△ABC中,∠A=90°.
(1)、在图上找到点O的位置 不写作法,但要标出字母 ,并写出点O的坐标;(2)、求点B绕着点O顺时针旋转到点E所经过的路径长.17. 如图,已知在△ABC中,∠A=90°. (1)、请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明);(2)、在(1)的条件下,若∠B=45°,AB=1,⊙P切BC于点D,求劣弧 的长.
(1)、请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明);(2)、在(1)的条件下,若∠B=45°,AB=1,⊙P切BC于点D,求劣弧 的长.
四、综合题
-
18. 如图,直径为1的圆从原点沿数轴向左滚动一周,圆上与原点重合的点O到达O′,设点O′表示的数为a.
 (1)、求a的值;(2)、求﹣(a﹣ )﹣π的算术平方根.19. 如图,PA是⊙O的切线,切点为A,AC是⊙O的直径,连接OP交⊙O于E.过A点作AB⊥PO于点D,交⊙O于B,连接BC,P B.
(1)、求a的值;(2)、求﹣(a﹣ )﹣π的算术平方根.19. 如图,PA是⊙O的切线,切点为A,AC是⊙O的直径,连接OP交⊙O于E.过A点作AB⊥PO于点D,交⊙O于B,连接BC,P B.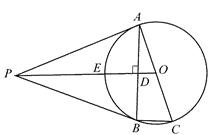 (1)、求证:PB是⊙O的切线;(2)、求证:E为△PAB的内心;(3)、若cos∠PAB= ,BC=1,求PO的长.20. 如图,△ABC是⊙O的内接三角形,AB为⊙O直径,AB=6,AD平分∠BAC,交BC于点E,交⊙O于点D,连接BD.
(1)、求证:PB是⊙O的切线;(2)、求证:E为△PAB的内心;(3)、若cos∠PAB= ,BC=1,求PO的长.20. 如图,△ABC是⊙O的内接三角形,AB为⊙O直径,AB=6,AD平分∠BAC,交BC于点E,交⊙O于点D,连接BD.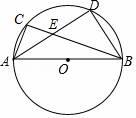 (1)、求证:∠BAD=∠CBD;(2)、若∠AEB=125°,求 的长(结果保留π).
(1)、求证:∠BAD=∠CBD;(2)、若∠AEB=125°,求 的长(结果保留π).