初中数学人教版九年级上学期 第二十四章 24.4 弧长和扇形的面积
试卷更新日期:2019-10-08 类型:同步测试
一、基础巩固
-
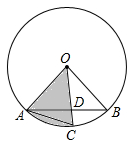
1. 如图,小正方形的边长均为1,扇形OAB是某圆锥的侧面展开图,则这个圆锥的底面周长为( )
 A、 B、 C、2 D、32. 已知扇形的弧长为 ,圆心角为120°,则它的半径为 。3. 已知一扇形的半径长是4,圆心角为60°,则这个扇形的面积为.4. 如图,一块六边形绿化园地,六角都做有半径为R的圆形喷水池,则这六个喷水池占去的绿化园地的面积为(结果保留 )
A、 B、 C、2 D、32. 已知扇形的弧长为 ,圆心角为120°,则它的半径为 。3. 已知一扇形的半径长是4,圆心角为60°,则这个扇形的面积为.4. 如图,一块六边形绿化园地,六角都做有半径为R的圆形喷水池,则这六个喷水池占去的绿化园地的面积为(结果保留 )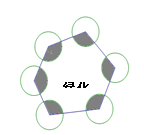 5. 如图,矩形ABCD中,以AD为直径的半圆与BC边相切于点E,且AD=8、AB=6,则图中阴影部分的面积是 .
5. 如图,矩形ABCD中,以AD为直径的半圆与BC边相切于点E,且AD=8、AB=6,则图中阴影部分的面积是 .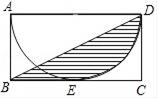
二、强化提升
-
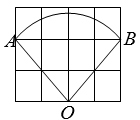
6. 如图,一根6m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动)那么小羊A在草地上的最大活动区域面积是( )
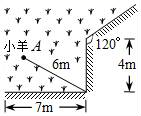 A、9πm2 B、 πm2 C、15πm2 D、 πm27. 如图,在Rt△ABC中,BC=3,∠BAC=30°,斜边AB的两个端点分别在相互垂直的射线OM,ON上滑动.下列结论:①若C、O两点关于AB对称,则OA=3 ;②若AB平分CO,则AB⊥CO;③C,O两点间的最大距离是6;④斜边AB的中点D运动的路径长是 π,其中正确的有( )
A、9πm2 B、 πm2 C、15πm2 D、 πm27. 如图,在Rt△ABC中,BC=3,∠BAC=30°,斜边AB的两个端点分别在相互垂直的射线OM,ON上滑动.下列结论:①若C、O两点关于AB对称,则OA=3 ;②若AB平分CO,则AB⊥CO;③C,O两点间的最大距离是6;④斜边AB的中点D运动的路径长是 π,其中正确的有( )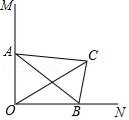 A、①② B、③④ C、②③④ D、①③④8. 如图,PA、PB是⊙O的两条切线,A、B是切点,PA= OA,阴影部分的面积为6π,则⊙O的半径长为 .
A、①② B、③④ C、②③④ D、①③④8. 如图,PA、PB是⊙O的两条切线,A、B是切点,PA= OA,阴影部分的面积为6π,则⊙O的半径长为 .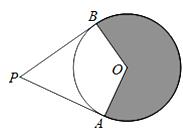 9.
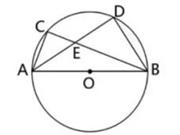
9.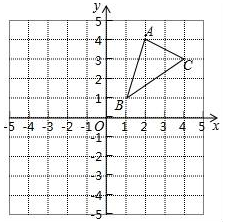 (1)、请画出△ABC关于x轴对称的△A1B1C1 , 并写出点A1的坐标.(2)、请画出△ABC绕点B逆时针旋转90°后的△A2BC2 .(3)、求出(2)中C点旋转到C2点所经过的路径长(结果保留根号和π).10. 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠1=∠C.
(1)、请画出△ABC关于x轴对称的△A1B1C1 , 并写出点A1的坐标.(2)、请画出△ABC绕点B逆时针旋转90°后的△A2BC2 .(3)、求出(2)中C点旋转到C2点所经过的路径长(结果保留根号和π).10. 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠1=∠C.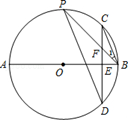 (1)、求证:CB∥PD;(2)、若∠1=22.5°,⊙O的半径R=2,求弧PCB与弦PB围成的弓形面积.
(1)、求证:CB∥PD;(2)、若∠1=22.5°,⊙O的半径R=2,求弧PCB与弦PB围成的弓形面积.三、真题演练
-
11. 若扇形的圆心角为90°,半径为6,则该扇形的弧长为( )A、 B、 C、 D、12. 如图,△ABC内接于⊙O,∠B=65°,∠C=70°,若BC=2 ,则 的长为( )
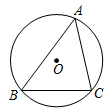 A、π B、 π C、2π D、 π13. 一个扇形的弧长是11πcm,半径是18cm,则此扇形的圆心角是度.
A、π B、 π C、2π D、 π13. 一个扇形的弧长是11πcm,半径是18cm,则此扇形的圆心角是度.