初中数学人教版九年级上学期 第二十四章 24.3 正多边形和圆
试卷更新日期:2019-10-08 类型:同步测试
一、基础巩固
-
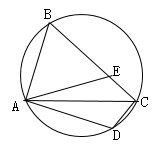
1. 如图,四边形ABCD内接于⊙O,若∠A=40°,则∠C=( )
 A、110° B、120° C、135° D、140°2. 半径为r的圆的内接正六边形边长为A、 B、 C、r D、2r3. 已知正多边形的一个外角是72°,则这个正多边形的边数是.4.(1)、已知三角形三个内角的度数比为1:2:3,求这个三角形三个外角的度数.(2)、一个正多边形的内角和为1800°,求这个多边形的边数.
A、110° B、120° C、135° D、140°2. 半径为r的圆的内接正六边形边长为A、 B、 C、r D、2r3. 已知正多边形的一个外角是72°,则这个正多边形的边数是.4.(1)、已知三角形三个内角的度数比为1:2:3,求这个三角形三个外角的度数.(2)、一个正多边形的内角和为1800°,求这个多边形的边数.二、强化提升
-
5. 已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示:按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转……连续经过六次旋转.在旋转的过程中,当正方形和正六边形的边重合时,点B,M间的距离可能是( )
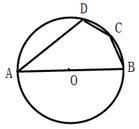
 A、0.5 B、0.7 C、 ﹣1 D、 ﹣16. 已知圆的半径是 ,则该圆的内接正六边形的面积是( )A、 B、 C、 D、7. 如图,五边形ABCDE是正五边形.若l1∥l2 , 则∠1-∠2=°.
A、0.5 B、0.7 C、 ﹣1 D、 ﹣16. 已知圆的半径是 ,则该圆的内接正六边形的面积是( )A、 B、 C、 D、7. 如图,五边形ABCDE是正五边形.若l1∥l2 , 则∠1-∠2=°.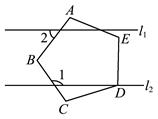 8. 如图,在正方形ABCD中,画一个最大的正六边形EFGHLJ,则∠BGF的度数是 .
8. 如图,在正方形ABCD中,画一个最大的正六边形EFGHLJ,则∠BGF的度数是 .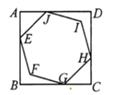 9. 如图,作半径为2的⊙O的内接正四边形ABCD,然后作正四边形ABCD的内切圆,得第二个圆,再作第二个圆的内接正四边形A1B1C1D1 , 又作正四边形A1B1C1D1的内切圆,得第三个圆…,如此下去,则第六个圆的半径为 .
9. 如图,作半径为2的⊙O的内接正四边形ABCD,然后作正四边形ABCD的内切圆,得第二个圆,再作第二个圆的内接正四边形A1B1C1D1 , 又作正四边形A1B1C1D1的内切圆,得第三个圆…,如此下去,则第六个圆的半径为 .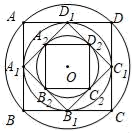 10. 如图,正五边形ABCD中,点F、G分别是BC、CD的中点,AF与BG相交于H.
10. 如图,正五边形ABCD中,点F、G分别是BC、CD的中点,AF与BG相交于H.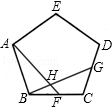 (1)、求证:△ABF≌△BCG;(2)、求∠AHG的度数.
(1)、求证:△ABF≌△BCG;(2)、求∠AHG的度数.三、真题演练
-
11. 正九边形的一个内角的度数是( )A、108° B、120° C、135° D、140°12. 下列命题是假命题的是( )A、三角形两边的和大于第三边 B、正六边形的每个中心角都等于60° C、半径为R的圆内接正方形的边长等于 R D、只有正方形的外角和等于360°13. 如图,在正六边形ABCDEF中,AC=2 ,则它的边长是( )
 A、1 B、 C、 D、2
A、1 B、 C、 D、2