初中数学人教版九年级上学期 第二十四章 24.2.1 点和圆的位置关系
试卷更新日期:2019-10-08 类型:同步测试
一、基础巩固
-
1. 若⊙O的半径为6,点P在⊙O内,则OP的长可能是( )A、5 B、6 C、7 D、82. 抢凳子是小时候常玩的游戏,人围成圈将凳子放在中间,主持人开始敲鼓,此时人围着凳子按同一方向转圈.当敲击声停止时,就要抢坐在凳子上,因为凳子数量少于玩游戏的总人数,未抢坐到凳子上的玩家淘汰下场.现在甲、乙、丙3位同学准备玩抢凳子的游戏,谁先抢坐到凳子上谁获胜.如图,三人已站定,主持人要在他们中间放一个凳子,为使游戏公平,凳子应放在图中三角形的 ( )
 A、三条高的交点 B、重心 C、内心 D、外心3. 下列尺规作图中,能确定圆心的是( )
A、三条高的交点 B、重心 C、内心 D、外心3. 下列尺规作图中,能确定圆心的是( )①如图1,在圆上任取三个点A,B,C,分别作弦AB,BC的垂直平分线,交点O即为圆心;②如图2,在圆上任取一点B,以B为圆心,小于直径长为半径画弧交圆于A,C两点,连结AB,BC,作∠ABC的平分线交圆于点D,作弦BD的垂直平分线交BD于点O,点O即为圆心;③如图3,在圆上截取弦AB=CD,连结AB,BC,CD,分别作∠ABC与∠DCB的平分线,交点O即为圆心.
 A、①② B、①③ C、②③ D、①②③4. 若圆的半径是 ,圆心的坐标是 ,点 的坐标是 ,则点 与 的位置关系是( )A、点P在⊙O外 B、点P在⊙O内 C、点P在⊙O上 D、点P在⊙O外或⊙O上5. 如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述何者正确( )
A、①② B、①③ C、②③ D、①②③4. 若圆的半径是 ,圆心的坐标是 ,点 的坐标是 ,则点 与 的位置关系是( )A、点P在⊙O外 B、点P在⊙O内 C、点P在⊙O上 D、点P在⊙O外或⊙O上5. 如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述何者正确( )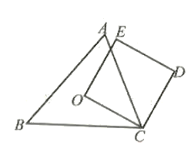 A、O是△AEB的外心,O是△AED的外心 B、O是△AEB的外心,O不是△AED的外心 C、O不是△AEB的外心,O是△AED的外心 D、O不是△AEB的外心,O不是△AED的外心6. 用反证法证明“如果lal>a,那么a<0.”是真命题时,第一步应先假设 .7. 如图,用尺规作出△ABC的外接圆⊙O,保留作图痕迹,不写作法.
A、O是△AEB的外心,O是△AED的外心 B、O是△AEB的外心,O不是△AED的外心 C、O不是△AEB的外心,O是△AED的外心 D、O不是△AEB的外心,O不是△AED的外心6. 用反证法证明“如果lal>a,那么a<0.”是真命题时,第一步应先假设 .7. 如图,用尺规作出△ABC的外接圆⊙O,保留作图痕迹,不写作法.
二、强化提升
-
8. 如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE、CD,PN、BF下列结论:①△ABE≌△DBC;②∠DFA=60°;③△BPN为等边三角形;④若∠1=∠2,则FB平分∠AFC.其中结论正确的有( )
 A、4个 B、3个 C、2个 D、1个9. 如图,点O1是△ABC的外心,以AB为直径作⊙O恰好过点O1 , 若AC=2,BC=4 ,则AO1的长是( )
A、4个 B、3个 C、2个 D、1个9. 如图,点O1是△ABC的外心,以AB为直径作⊙O恰好过点O1 , 若AC=2,BC=4 ,则AO1的长是( )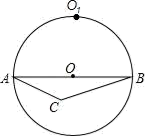 A、3 B、 C、2 D、210. 如图, 中, 是 内部的一个动点,且满足 ,则线段 长的最小值为( )
A、3 B、 C、2 D、210. 如图, 中, 是 内部的一个动点,且满足 ,则线段 长的最小值为( )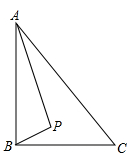 A、 B、 C、 D、11. 如图,四边形ABCD为圆内接四边形,对角线AC、BD交于点E,延长DA、CB交于点F,且∠CAD=60°,DC=DE.
A、 B、 C、 D、11. 如图,四边形ABCD为圆内接四边形,对角线AC、BD交于点E,延长DA、CB交于点F,且∠CAD=60°,DC=DE.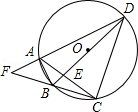
求证:
(1)、AB=AF;(2)、A为△BEF的外心(即△BEF外接圆的圆心).三、真题演练