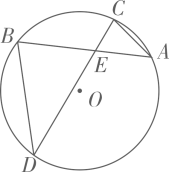初中数学人教版九年级上学期 第二十四章 24.1.4 圆周角
试卷更新日期:2019-10-08 类型:同步测试
一、基础巩固
-
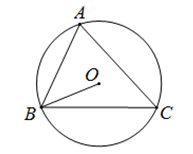
1. 如图,△ABC内接于⊙O,∠A=68°,则∠OBC等于( )
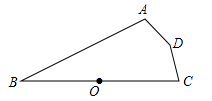
 A、22° B、26° C、32° D、34°2. 如图,点A,B,C在⊙O上,AB∥CO,∠B=22°,则∠A=( ).
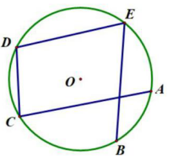
A、22° B、26° C、32° D、34°2. 如图,点A,B,C在⊙O上,AB∥CO,∠B=22°,则∠A=( ).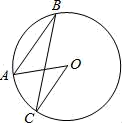 A、22° B、40° C、44° D、68°3. 如图,四边形ABCD是⊙O的内接四边形,若∠A=70°,则∠C的度数是( )
A、22° B、40° C、44° D、68°3. 如图,四边形ABCD是⊙O的内接四边形,若∠A=70°,则∠C的度数是( )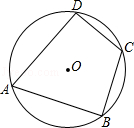 A、100° B、110° C、120° D、130°4. 如图,AB是⊙O的直径,点C在⊙O上,弦BD平分∠ABC,则下列结论错误的是
A、100° B、110° C、120° D、130°4. 如图,AB是⊙O的直径,点C在⊙O上,弦BD平分∠ABC,则下列结论错误的是 A、AD=DC B、
A、AD=DC B、 C、∠ADB=∠ACB
D、∠DAB=∠CBA
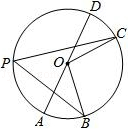
5. 如图,O是⊙O的圆心,点A、B、C在⊙O上,AO∥BC,∠AOB=38º,则∠OAC的度数是.
C、∠ADB=∠ACB
D、∠DAB=∠CBA
5. 如图,O是⊙O的圆心,点A、B、C在⊙O上,AO∥BC,∠AOB=38º,则∠OAC的度数是.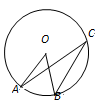 6. 如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,∠BCD=130°,则∠ABD的度数是 .
6. 如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,∠BCD=130°,则∠ABD的度数是 .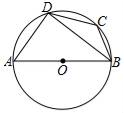 7. 如图,⊙D是△ABC的外接圆,AB=AC,P是⊙O上一点.请你只用无刻度的直尺,分别画出图①和图②中∠P的平分线,保留画图痕迹.
7. 如图,⊙D是△ABC的外接圆,AB=AC,P是⊙O上一点.请你只用无刻度的直尺,分别画出图①和图②中∠P的平分线,保留画图痕迹.
二、强化提升
-
8. 如图,矩形ABCD中,点E,F分别在边AD,CD上,且EF⊥BE,EF=BE,△DEF的外接圆⊙O恰好切BC于点G,BF交⊙O于点H,连结DH.若AB=8,则DH=.
 9. 如图,已知四边形ABCD内接于半径为4的⊙O中,且∠C=2∠A,则BD=.
9. 如图,已知四边形ABCD内接于半径为4的⊙O中,且∠C=2∠A,则BD=.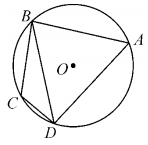 10. 如图,AB为⊙O的直径,C为⊙O上一点,∠BOC=50°,AD∥OC,AD交⊙O于点D,连接AC,CD,那么∠ACD= .
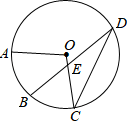
10. 如图,AB为⊙O的直径,C为⊙O上一点,∠BOC=50°,AD∥OC,AD交⊙O于点D,连接AC,CD,那么∠ACD= . 11. 如图,AB是 的直径,点C、D是 两点,且AC=CD.求证:OC//BD.
11. 如图,AB是 的直径,点C、D是 两点,且AC=CD.求证:OC//BD.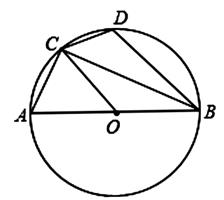 12. 如图,AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,OD⊥BC于E.
12. 如图,AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,OD⊥BC于E. (1)、求证:OD∥AC;(2)、若BC=8,DE=3,求⊙O的直径.
(1)、求证:OD∥AC;(2)、若BC=8,DE=3,求⊙O的直径.三、真题演练