初中数学人教版九年级上学期 第二十三章测试卷
试卷更新日期:2019-10-08 类型:单元试卷
一、单选题
-
1. 下列电视台的台标中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图的四个图形中,由基础图形通过平移、旋转或轴对称这三种变换都能得到的是( )A、
2. 如图的四个图形中,由基础图形通过平移、旋转或轴对称这三种变换都能得到的是( )A、 B、
B、 C、
C、 D、
D、 3. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、线段 B、直角三角形 C、等边二角形 D、平行四边形4. 在平面直角坐标系内,点(-1,2)关于原点对称的点的坐标是( )A、(2,-1) B、(1,2) C、(1,-2) D、(-1,-2)5. 在平面直角坐标系中,点 的坐标为 ,以原点为中心,将点 顺时针旋转 得到点 ,则点 的坐标为( )A、 B、 C、 D、6. 如图, 的斜边在 轴上, ,含 角的顶点与原点重合,直角顶点 在第二象限,将 绕原点顺时针旋转 后得到 ,则 点的对应点 的坐标是( )
3. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、线段 B、直角三角形 C、等边二角形 D、平行四边形4. 在平面直角坐标系内,点(-1,2)关于原点对称的点的坐标是( )A、(2,-1) B、(1,2) C、(1,-2) D、(-1,-2)5. 在平面直角坐标系中,点 的坐标为 ,以原点为中心,将点 顺时针旋转 得到点 ,则点 的坐标为( )A、 B、 C、 D、6. 如图, 的斜边在 轴上, ,含 角的顶点与原点重合,直角顶点 在第二象限,将 绕原点顺时针旋转 后得到 ,则 点的对应点 的坐标是( )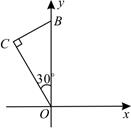 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 如图,正方形ABCD的边长为4,点E是CD的中点,AF平分∠BAE交BC于点F,将△ADE绕点A顺时针旋转90°得△ABG,则CF的长为.
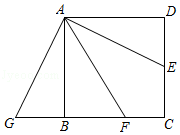 8. 如图所示的图案是由全等的图形拼成的,其中AD=0.5cm,BC=1cm,则AF=cm.
8. 如图所示的图案是由全等的图形拼成的,其中AD=0.5cm,BC=1cm,则AF=cm. 9. 如图,正方形ABCD可以看作由什么“基本图形”经过怎样的变化形成的? .
9. 如图,正方形ABCD可以看作由什么“基本图形”经过怎样的变化形成的? .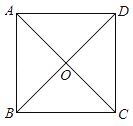
三、作图题
-
10. 如图,4×6的正方形网格中,每个小正方形的顶点称为格点,A,B,C均为格点。在下列各图中画出四边形ABCD,使点D也为格点,且四边形ABCD分别符合下列条件:
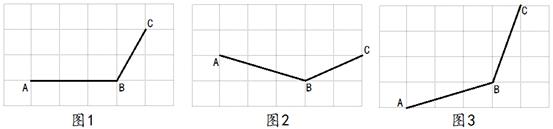 (1)、是中心对称图形(画在图1中)(2)、是轴对称图形(画在图2中)(3)、既是轴对称图形,又是中心对称图形(画在图3中)11. 如图,请在图中按要求解答下面问题
(1)、是中心对称图形(画在图1中)(2)、是轴对称图形(画在图2中)(3)、既是轴对称图形,又是中心对称图形(画在图3中)11. 如图,请在图中按要求解答下面问题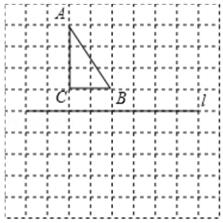
①作出三角形ABC关于直线l对称的三角形A1B1C1;
②作出将三角形ABC绕着点B顺时针旋转90度得到的三角形A2BC2
12. 已知:在平面直角坐标系中, 的三个顶点的坐标分别为 , , .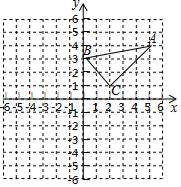
①画出 关于原点成中心对称的 ,并写出点 的坐标;
②画出将 绕点 按顺时针旋转 所得的 .
13. 已知在图(1)与图(2)中,每个小方格都是边长为1个单位的正方形, 的三个顶点都在格点上.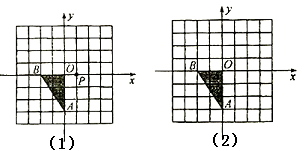 (1)、将 关于点 对称,在图(1)中画出对称后的图形 ,并涂黑;(2)、将△OAB先向右平移3个单位,再向上平移2个单位,在图2中画出平移后的图形,并涂黑。
(1)、将 关于点 对称,在图(1)中画出对称后的图形 ,并涂黑;(2)、将△OAB先向右平移3个单位,再向上平移2个单位,在图2中画出平移后的图形,并涂黑。四、综合题
-
14. 在平面直角坐标系 中,已知A(﹣1,5),B(4,2),C(﹣1,0)三点.点A关于原点O的对称点A′,点B关于 轴的对称点为B′,点C关于 轴的对称点为C′.(1)、A′的坐标为 , B′的坐标为 , C′的坐标为 .(2)、建立平面直角坐标系,描出以下三点A、B′、C′,并求△AB′C′的面积.15. 如图1是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=30,DM=10.
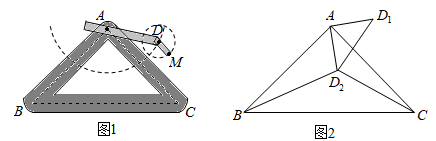 (1)、在旋转过程中,
(1)、在旋转过程中,①当A,D,M三点在同一直线上时,求AM的长。
②当A,D,M三点为同一直角三角形的顶点时,求AM的长。
(2)、若摆动臂AD顺时针旋转90°,点D的位置由△ABC外的点D1转到其内的点D2处,连结D1D2 , 如图2.此时∠AD2C=135°,CD2=60,求BD2的长.