江苏省扬州市江都区邵樊片2019届九年级上学期数学第一次月考试卷

试卷更新日期：2019-09-30 类型：月考试卷

进入出卷网下载

一、单选题

1. $⊙ O$ 的半径为5，圆心O到直线l的距离为3，则直线l与 $⊙ O$ 的位置关系是 $($ $)$

A、相交 B、相切 C、相离 D、无法确定

查看试题解析
2. 如图，点A，B，C在 $⊙ O$ 上， $∠ ACB = 35^{\circ}$ ，则 $∠ AOB$ 的度数是 $($ $)$

A、 $75^{\circ}$ B、 $70^{\circ}$ C、 $65^{\circ}$ D、 $35^{\circ}$

查看试题解析
3. AB是⊙O的直径，点C在圆上，∠ABC=65°，那么∠OCA的度数是（）

A、25° B、35° C、15° D、20°

查看试题解析
4. 用配方法解一元二次方程 $x^{2} + 8 x + 9 = 0$ ，下列变形正确的是 $($ $)$

A、 ${(x + 4)}^{2} = - 7$ B、 ${(x - 4)}^{2} = 7$ C、 ${(x + 4)}^{2} = 7$ D、 ${(x - 4)}^{2} = 25$

查看试题解析
5. 某企业2018年初获利润300万元，到2020年初计划利润达到507万元.设这两年的年利润平均增长率为x.应列方程是（）

A、300（1+x）=507 B、300（1+x）²=507 C、300（1+x）+300（1+x）²=507 D、300+300（1+x）+300（1+x）²=507

查看试题解析
6. 如图，直线AB与⊙O相切于点A，AC、CD是⊙O的两条弦，且CD∥AB，若⊙O的半径为5，CD=8，则弦AC的长为（）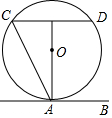

A、10 B、8 C、4 $\sqrt{3}$ D、4 $\sqrt{5}$

查看试题解析
7. 已知⊙O的半径为10，圆心O到弦AB的距离为5，则弦AB所对的圆周角的度数是（）

A、30° B、60° C、30°或150° D、60°或120°

查看试题解析
8. 在△ABC中，若O为BC边的中点，则必有：AB²+AC²=2AO²+2BO²成立.依据以上结论，解决如下问题：如图，在矩形DEFG中，已知DE=4，EF=3，点P在以DE为直径的半圆上运动，则PF²+PG²的最小值为（）

A、 $\sqrt{10}$ B、 $\frac{19}{2}$ C、34 D、10

查看试题解析

二、填空题

9. 已知关于x的一元二次方程x²+kx﹣6=0有一个根为﹣3，则方程的另一个根为．

查看试题解析
10. 如图，在扇形CAB中，CD⊥AB，垂足为D，⊙E是△ACD的内切圆，连接AE，BE，则∠AEB的度数为.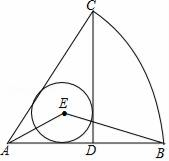

查看试题解析
11. 如图，正方形ABCD的边长为8，M是AB的中点，P是BC边上的动点，连结PM，以点P为圆心，PM长为半径作 $⊙ P .$ 当 $⊙ P$ 与正方形ABCD的边相切时，BP的长为．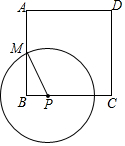

查看试题解析

三、解答题

12. 如图，已知A、B、C、D、E是⊙O上五点，⊙O的直径BE=2 $\sqrt{3}$ ，∠BCD=120°，A为 $\vec{B E}$ 的中点，延长BA到点P，使BA=AP，连接PE.

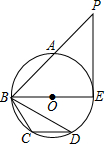(1)、求线段BD的长；

(2)、求证：直线PE是⊙O的切线.

查看试题解析
13. 解方程：

(1)、 $x^{2} + x - 2 = 0$

(2)、 $2 (x - 3) = 3 x (x - 3)$ .

查看试题解析
14. 关于 $x$ 的一元二次方程 $a x^{2} + b x + 1 = 0$ ．

(1)、当 $b = a + 2$ 时，利用根的判别式判断方程根的情况；

(2)、若方程有两个相等的实数根，写出一组满足条件的 $a$ ， $b$ 的值，并求此时方程的根．

查看试题解析
15. 童装店销售某款童装，每件售价为60元，每星期可卖100件，为了促销，该店决定降价销售，经市场调查反应：每降价1元，每星期可多卖10件 $.$ 已知该款童装每件成本30元 $.$ 设该款童装每件售价x元，每星期的销售量为y件.

(1)、求y与x之间的函数关系式 $($ 不求自变量的取值范围 $)$ ；

(2)、当每件童装售价定为多少元时，该店一星期可获得3910元的利润？

查看试题解析
16. 已知 $A B$ 是 $⊙ O$ 的直径，弦 $C D$ 与 $A B$ 相交， $∠ B A C = 38 °$ .

(1)、如图①，若 $D$ 为 $\overset{⌢}{A B}$ 的中点，求 $∠ A B C$ 和 $∠ A B D$ 的大小；

(2)、如图②，过点 $D$ 作 $⊙ O$ 的切线，与 $A B$ 的延长线交于点 $P$ ，若 $D P / / A C$ ，求 $∠ O C D$ 的大小.

查看试题解析
17. 如图，在△ABC中，∠ACB=90°，以点B为圆心，BC长为半径画弧，交边AB与点D，以A为圆心，AD长为半径画弧，交边AC于点E，连接CD.

(1)、若∠A=28°，求∠ACD的度数；

(2)、设BC=a，AC=b.
①线段AD的长是方程 $x^{2} + 2 a x - b^{2} = 0$ 的一个根吗？为什么？

②若AD=EC，求 $\frac{a}{b}$ 的值.

查看试题解析
18. 如图，在△ABC中，AB=AC，以AB为直径的圆交AC于点D，交BC于点E，延长AE至点F，使EF=AE，连接FB，FC.

(1)、求证：四边形ABFC是菱形；

(2)、若AD=7，BE=2，求半圆和菱形ABFC的面积.

查看试题解析
19. 如图，已知D，E分别为△ABC的边AB，BC上两点，点A，C，E在⊙D上，点B，D在⊙E上.F为 $\vec{B D}$ 上一点，连接FE并延长交AC的延长线于点N，交AB于点M.

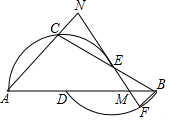(1)、若∠EBD为α，请将∠CAD用含α的代数式表示；

(2)、若EM=MB，请说明当∠CAD为多少度时，直线EF为⊙D的切线；

(3)、在（2）的条件下，若AD= $\sqrt{3}$ ，求 $\frac{M N}{M F}$ 的值.

查看试题解析
20. 已知四边形ABCD是⊙O的内接四边形，AC是⊙O的直径，DE⊥AB，垂足为E.

(1)、延长DE交⊙O于点F，延长DC，FB交于点P，如图1.求证：PC=PB；

(2)、过点B作BG⊥AD，垂足为G，BG交DE于点H，且点O和点A都在DE的左侧，如图2.若AB= $\sqrt{3}$ ，DH=1，∠OHD=80°，求∠BDE的大小.

查看试题解析
21. 问题提出
图① 图②

图③

(1)、如图①，在△ABC中，∠A＝120°，AB＝AC＝5，求△ABC的外接圆半径R的值。

(2)、如图②，⊙O的半径为13，弦AB＝24，M是AB的中点，P是⊙O上一动点，求PM的最大值.

(3)、如图③所示，AB、AC、BC是某新区的三条规划路其中，AB＝6km，AC＝3km，∠BAC＝60°，BC所对的圆心角为60°.新区管委会想在BC路边建物资总站点P，在AB、AC路边分别建物资分站点E、F.也就是，分别在 $\vec{B C}$ 、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输，因此，要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短，试求PE＋EF＋FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).

查看试题解析