江苏省兴化市顾庄学区2019届九年级上学期数学第三次月考试卷
试卷更新日期:2019-09-30 类型:月考试卷
一、单选题
-
1. 一种零件的长是2毫米,在一幅设计图上的长是40厘米,这幅设计图的比例尺是( )A、200:1 B、2000:1 C、1:2000 D、1:2002. 若P是线段AB的黄金分割点(PA>PB),设AB=1,则PA的长约为( ).A、0.191 B、0.382 C、0.5 D、0.6183. 图中四个阴影的三角形中与△ABC相似的是( )
 A、
A、 B、
B、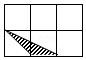 C、
C、 D、
D、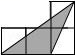 4. 若△ABC∽△DEF,相似比为3:2,则对应面积的比为( )A、3:2 B、3:5 C、9:4 D、4:95. 从地面竖直向上抛出一小球,小球的高度 米 与小球运动的时间 秒 之间的关系式为 若小球在第7秒与第14秒时的高度相同,则在下列时间中小球所在高度最高的是A、第8秒 B、第10秒 C、第12秒 D、第15秒6. 如图,以某点为位似中心,将△OAB进行位似变换得到△DFE,若△OAB与△DFE的相似比为k,则位似中心的坐标与k的值分别为( )
4. 若△ABC∽△DEF,相似比为3:2,则对应面积的比为( )A、3:2 B、3:5 C、9:4 D、4:95. 从地面竖直向上抛出一小球,小球的高度 米 与小球运动的时间 秒 之间的关系式为 若小球在第7秒与第14秒时的高度相同,则在下列时间中小球所在高度最高的是A、第8秒 B、第10秒 C、第12秒 D、第15秒6. 如图,以某点为位似中心,将△OAB进行位似变换得到△DFE,若△OAB与△DFE的相似比为k,则位似中心的坐标与k的值分别为( )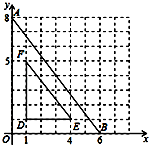 A、(2,2),2 B、(0,0),2 C、(2,2), D、(0,0),
A、(2,2),2 B、(0,0),2 C、(2,2), D、(0,0),二、填空题
-
7. 将抛物线y=(x-3)2+1先向上平移2个单位,再向左平移1个单位后,得到的抛物线解析式为.8. 如图,添加一个条件: , 使△ADE∽△ACB,(写出一个即可)
 9. 如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,DB=2,则CD的长为 .
9. 如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,DB=2,则CD的长为 . 10. 已知 ,则 =.11. 在平行四边形ABCD中,E在DC上,若DE:EC=1:2,则BF:BE=.
10. 已知 ,则 =.11. 在平行四边形ABCD中,E在DC上,若DE:EC=1:2,则BF:BE=. 12. 如图,l1∥l2∥l3 , 两条直线与这三条平行线分别交于点A、B、C和D、E、F,已知 ,若DF=10,则DE=.
12. 如图,l1∥l2∥l3 , 两条直线与这三条平行线分别交于点A、B、C和D、E、F,已知 ,若DF=10,则DE=.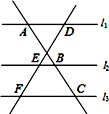 13. 如图,放映幻灯片时,通过光源把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为20cm,到屏幕的距离为30cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为.
13. 如图,放映幻灯片时,通过光源把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为20cm,到屏幕的距离为30cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为.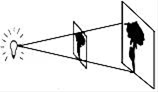 14. 已知抛物线y=x2﹣x﹣1与x轴的一个交点为(m,0),则代数式m2﹣m+2018的值为.15. 若关于x的函数y=kx2+2x﹣1与x轴仅有一个公共点,则实数k的值为 .16. 已知点A,B的坐标分别为(1,0),(2,0).若二次函数y=x2+(a﹣3)x+3的图象与线段AB只有一个交点,则a的取值范围是.
14. 已知抛物线y=x2﹣x﹣1与x轴的一个交点为(m,0),则代数式m2﹣m+2018的值为.15. 若关于x的函数y=kx2+2x﹣1与x轴仅有一个公共点,则实数k的值为 .16. 已知点A,B的坐标分别为(1,0),(2,0).若二次函数y=x2+(a﹣3)x+3的图象与线段AB只有一个交点,则a的取值范围是.三、解答题
-
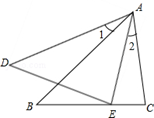
17. 如图,AB•AE=AD•AC,且∠1=∠2,求证:△ABC∽△ADE.
 18. 如图,两个全等的等腰直角三角形按照如图放置,图中有几组相似三角形(不包括全等三角形)?请分别写出来,选择其中的一组证明.
18. 如图,两个全等的等腰直角三角形按照如图放置,图中有几组相似三角形(不包括全等三角形)?请分别写出来,选择其中的一组证明.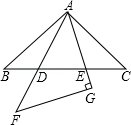 19. 如图,已知△ABC∽△ADE,AB=30cm,BD=18cm,BC=20cm,∠BAC=75°,∠ABC=40°.
19. 如图,已知△ABC∽△ADE,AB=30cm,BD=18cm,BC=20cm,∠BAC=75°,∠ABC=40°.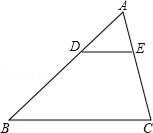
求:
(1)、∠ADE和∠AED的度数;(2)、DE的长.20. 如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.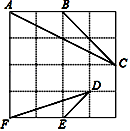 (1)、填空:∠ABC=°,AC=;(2)、判断:△ABC与△DEF是否相似,并证明你的结论.21. 某商店经营一种小商品,进价为40元,据市场调查,销售价是60元时,平均每天销售量是300件,而销售价每降低1元,平均每天就可以多售出20件.(1)、假定每件商品降价x元,商店每天销售这种小商品的利润是y元,请写出y与x间的函数关系式;(2)、每件小商品销售价是多少元时,商店每天销售这种小商品的利润最大?最大利润是多少?22. 如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,设运动的时间为t.
(1)、填空:∠ABC=°,AC=;(2)、判断:△ABC与△DEF是否相似,并证明你的结论.21. 某商店经营一种小商品,进价为40元,据市场调查,销售价是60元时,平均每天销售量是300件,而销售价每降低1元,平均每天就可以多售出20件.(1)、假定每件商品降价x元,商店每天销售这种小商品的利润是y元,请写出y与x间的函数关系式;(2)、每件小商品销售价是多少元时,商店每天销售这种小商品的利润最大?最大利润是多少?22. 如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,设运动的时间为t.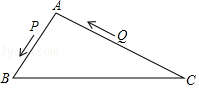 (1)、用含t的代数式表示:AP= , AQ=.(2)、当以A,P,Q为顶点的三角形与△ABC相似时,求运动时间是多少?23. 河上有一座桥孔为抛物线形的拱桥(如图1),水面宽6m时,水面离桥孔顶部3m,因降暴雨水面上升1m.
(1)、用含t的代数式表示:AP= , AQ=.(2)、当以A,P,Q为顶点的三角形与△ABC相似时,求运动时间是多少?23. 河上有一座桥孔为抛物线形的拱桥(如图1),水面宽6m时,水面离桥孔顶部3m,因降暴雨水面上升1m.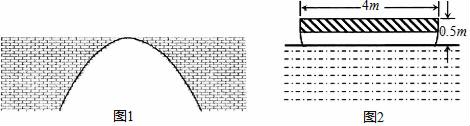 (1)、建立适当的坐标系,并求暴雨后水面的宽;(2)、一艘装满物资的小船,露出水面部分高为0.5m、宽4m(横断面如图2所示),暴雨后这艘船能从这座拱桥下通过吗?
(1)、建立适当的坐标系,并求暴雨后水面的宽;(2)、一艘装满物资的小船,露出水面部分高为0.5m、宽4m(横断面如图2所示),暴雨后这艘船能从这座拱桥下通过吗?(注:结果保留根号.)
24. 一块直角三角形的木板,它的一条直角边AC长为1.5米,面积为1.5平方米.现在要把它加工成一个正方形桌面,甲、乙两人的加工方法分别如图(ⅰ)、(ⅱ)所示,记两个正方形面积分别为S1、S2 , 请通过计算比较S1与S2的大小.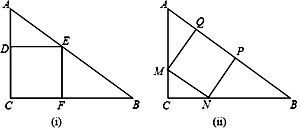 25. 如图,已知AB⊥BC,CD⊥BC,AB=4,CD=2.P为线段BC上的点,设BC=m.
25. 如图,已知AB⊥BC,CD⊥BC,AB=4,CD=2.P为线段BC上的点,设BC=m. (1)、若m=9,
(1)、若m=9,①若△BAP∽△CDP,求线段BP的长;
②若△BAP∽△CPD,求线段BP的长;
(2)、试求m为何值时,使得△BAP与△CDP相似的点P有且只有2个.26. 已知抛物线y=ax2+bx+c经过A(0,2),B(2,﹣2)两点.(1)、用含a的式子表示b.(2)、当a=﹣ 时,y=ax2+bx+c的函数值为正整数,求满足条件的x值.(3)、若a>0,线段AB下方的抛物线上有一点E,求证:不管a取何值,当△EAB的面积最大时,E点的横坐标为定值.