江苏省南京市建邺区2019届九年级上学期数学10月月考试卷

试卷更新日期：2019-09-30 类型：月考试卷

进入 出卷网 下载

一、单选题

  • 1. 下列方程中，是一元二次方程的是（    ）
    A、x2﹣5x＝0 B、x+1＝0 C、y﹣2x＝0 D、2x3﹣2＝0

    查看试题解析

  • 2. 若关于x的一元二次方程x2﹣2x+m=0有一个解为x=﹣1，则另一个解为（   ）
    A、1 B、﹣3 C、3 D、4

    查看试题解析

  • 3. 如图，AB是⊙O的弦，半径OC⊥AB于点D，下列判断中错误的是（   ）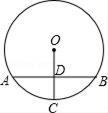

    A、OD＝DC B、弧AC=弧BC C、AD＝BD D、∠AOC= 12 ∠AOB

    查看试题解析

  • 4. 小亮是一名职业足球队员，根据以往比赛数据统计，小亮进球率为 10% ，他明天将参加一场比赛，下面几种说法正确的是（ ）
    A、小亮明天的进球率为 10% B、小亮明天每射球10次必进球1次 C、小亮明天有可能进球 D、小亮明天肯定进球

    查看试题解析

  • 5. 如图是一个餐盘，它的外围是由以正三角形的顶点为圆心，以正三角形的边长为半径的三段等弧组成，已知正三角形的边长为10，则该餐盘的面积是（   ）

    A、50π-50 3 B、50π–25 3 C、25π＋50 3 D、50π

    查看试题解析

  • 6. 如图，△ABC是一张三角形纸片，⊙O是它的内切圆，点D、E是其中的两个切点，已知AD=6cm，小明准备用剪刀沿着与⊙O相切的一条直线MN剪下一块三角形（△AMN），则剪下的△AMN的周长是（   ）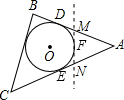

    A、9cm B、12cm C、15cm D、18cm

    查看试题解析

二、填空题

  • 7. 若（x﹣1）2=4，则x= ．

    查看试题解析

  • 8. ⊙O的半径为10cm，A、B、C三点到圆心O的距离分别为8cm、10cm、12cm，则点A、B、C与⊙O的位置关系是：点A在；点B在；点C在.

    查看试题解析

  • 9. 已知扇形的圆心角为120°，半径6cm，则扇形的弧长为cm，扇形的面积为cm2.

    查看试题解析

  • 10. 袋中装有6个黑球和n个白球，经过若干次试验，发现“若从袋中任摸出一个球，恰是黑球的概率为 34 ，则这个袋中白球大约有个．

    查看试题解析

  • 11. 为了了解贯彻执行国家提倡的“阳光体育运动”的实施情况，将某班50名同学一周的体育锻炼情况绘制成了如图所示的条形统计图，根据提供的数据，该班50名同学一周参加体育锻炼时间的中位数是 ， 众数是.

    查看试题解析

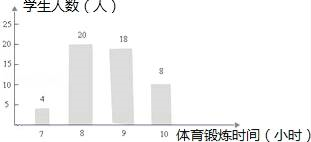  • 12. 如图，点E是正方形ABCD的边CD上一点，以A为圆心，AB为半径的弧与BE交于点F，则∠EFD＝°.

    查看试题解析

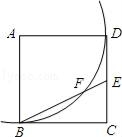  • 13. 若关于x的一元二次方程 12 x2﹣2mx﹣4m+1=0有两个相等的实数根，则（m﹣2）2﹣2m（m﹣1）的值为.

    查看试题解析

  • 14. 如图，⊙O是△ABC的外接圆，连接OA、OB，∠ACB=40°，则∠ABO的大小为度.

    查看试题解析

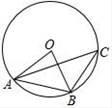  • 15. 如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=2.点P是△ABC内部的一个动点，且满足∠PAC=∠PCB，则线段BP长的最小值是.

    查看试题解析

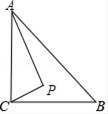  • 16. 对于两个不相等的实数a、b，我们规定：符号Max{a，b}表示a、b中的较大数，如：Max{﹣2，﹣4}=﹣2.按照这个规定，方程Max{x，﹣x}= 2x+1x 的解为.

    查看试题解析

三、解答题

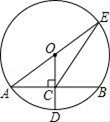
  • 17. 用公式法解一元二次方程：2x2﹣7x+6＝0.

    查看试题解析

  • 18. 解方程：x2－4x－5＝0

    查看试题解析

  • 19. 某景区商店以2元的批发价进了一批纪念品.经调查发现，每个定价3元，每天可以能卖出500件，而且定价每上涨0.1元，其销售量将减少10件.根据规定：纪念品售价不能超过批发价的2.5倍.
    (1)、当每个纪念品定价为3.5元时，商店每天能卖出件；
    (2)、如果商店要实现每天800元的销售利润，那该如何定价？

    查看试题解析

  • 20. 如图，⊙O的半径OD⊥弦AB于点C，连接AO并延长交⊙O于点E，连接EC，若AB＝8，CD＝2，求⊙O的半径及EC的长.

    查看试题解析

  • 21. 如图所示：爬上小山有甲、乙两条石阶路.运用所学统计知识解答下列问题：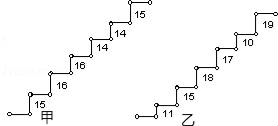

    (1)、哪条路走起来更舒适？
    (2)、设计一条舒适的石阶路，简要说明理由.

    查看试题解析

  • 22. 小明参加某个智力竞答节目，答对最后两道单选题就顺利通关．第一道单选题有3个选项，第二道单选题有4个选项，这两道题小明都不会，不过小明还有一个“求助”没有用（使用“求助”可以让主持人去掉其中一题的一个错误选项）．
    (1)、如果小明第一题不使用“求助”，那么小明答对第一道题的概率是 ．
    (2)、如果小明将“求助”留在第二题使用，请用树状图或者列表来分析小明顺利通关的概率．
    (3)、从概率的角度分析，你建议小明在第几题使用“求助”．（直接写出答案）

    查看试题解析

  • 23. “三八宏图展，九州春意浓”，为了解某校1000名学生在2017年3月8日“妇女节”期间对母亲表达祝贺的方式，某班兴趣小组随机抽取了部分学生进行问卷调查，并将问卷调查的结果绘制成如下不完整的统计表：

    某校抽取学生“妇女节”期间对母亲表达祝贺的方式的统计表

    方式

    频数

    百分比

    送母亲礼物

    23

    46%

    帮母亲做家务

    给母亲一个爱的拥抱

    8%

    其他

    15

    合计

    100%
    (1)、本次问卷调查抽取的学生共有人，其中通过给母亲一个爱的拥抱表达祝贺的学生有人.
    (2)、从上表的“频数”、“百分比”两列数据中选择一列，用适当的统计图表示.
    (3)、根据抽样的结果，估计该校学生通过帮母亲做家务表达祝贺的约有多少人？

    查看试题解析

  • 24. 水果店张阿姨以每斤2元的价格购进某种水果若干斤，然后以每斤4元的价格出售，每天可售出100斤，通过调查发现，这种水果每斤的售价每降低0.1元，每天可多售出20斤，为保证每天至少售出260斤，张阿姨决定降价销售.
    (1)、若将这种水果每斤的售价降低x元，则每天的销售量是斤（用含x的代数式表示）；
    (2)、销售这种水果要想每天盈利300元，张阿姨需将每斤的售价降低多少元？

    查看试题解析

  • 25. 如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过点D作DE⊥AC，交AC于点E，AC的反向延长线交⊙O于点F.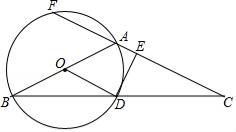

    (1)、求证：DE是⊙O的切线.
    (2)、若DE+EA=4，⊙O的半径为5，求CF的长度.

    查看试题解析

  • 26. 阅读下面材料：

    在学习《圆》这一章时，老师给同学们布置了一道尺规作图题：

    尺规作图：过圆外一点作圆的切线.

    已知：P为⊙O外一点.

    求作：经过点P的⊙O的切线.

    小敏的作法如下：如图，

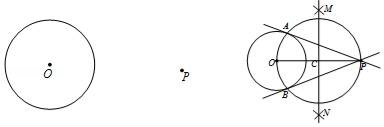
    ①连接OP，作线段OP的垂直平分线MN交OP于点C.

    ②以点C为圆心，CO的长为半径作圆，交⊙O于A，B两点.

    ③作直线PA，PB.

    老师认为小敏的作法正确.

    请回答：连接OA，OB后，可证∠OAP=∠OBP=90°，其依据是；由此可证明直线PA，PB都是⊙O的切线，写出依据.请写出证明过程.

    查看试题解析

  • 27. 已知△ABC中，∠CAB=90°，AC=AB=3，△CDE中，∠CDE=90°，CD=DE=5，连接BE，取BE中点F，连接AF、DF.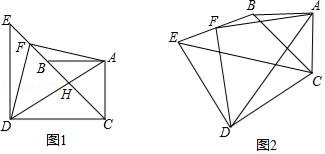

    (1)、如图1，若C、B、E三点共线，H为BC中点.

    ①直接指出AF与DF的关系；

    ②直接指出FH的长度；

    (2)、将图（1）中的△CDE绕C点逆时针旋转a（如图2，0°＜α＜180°），试确定AF与DF的关系，并说明理由；
    (3)、在（2）中，若AF= 722 ，请直接指出点F所经历的路径长.

    查看试题解析