江苏省东台市第二联盟2019届九年级上学期数学12月月考试卷

试卷更新日期：2019-09-30 类型：月考试卷

进入出卷网下载

一、单选题

1. 盒子中装有2个红球和4个绿球,每个球除颜色外完全相同,从盒子中任意摸出一个球,是绿球的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{1}{2}$

查看试题解析
2. 抛物线y＝－x²不具有的性质是（）

A、开口向下 B、对称轴是y轴 C、与y轴不相交 D、最高点是原点

查看试题解析
3. 在半径为1的⊙O中，120°的圆心角所对的弧长是（）

A、 $\frac{π}{3}$ B、 $\frac{2 π}{3}$ C、 $π$ D、 $\frac{3 π}{2}$

查看试题解析
4. △ABC中，∠B=90°，AB=1，BC=2，则sinA=（）

A、 $\frac{\sqrt{5}}{2}$ B、 $\frac{1}{2}$ C、 $\frac{2 \sqrt{5}}{5}$ D、 $\frac{\sqrt{5}}{5}$

查看试题解析
5. 已知二次函数y=ax²+bx+c（a＜0）的图象经过点A（－2，0）、O（0，0）、B（－3，y₁）、C（3，y₂）四点，则y₁与y₂的大小关系正确的是（　）

A、y₁＜y₂ B、y₁＞y₂ C、y₁＝y₂ D、不能确定

查看试题解析
6. 如图，D、E分别是△ABC的边AB、BC上的点，且DE∥AC，AE、CD相交于点O，若S_△_DOE：S_△_COA=1：25，则S_△_BDE与S_△_CDE的比是（）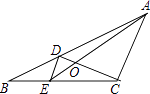

A、1：3 B、1：4 C、1：5 D、1：25

查看试题解析

二、填空题

7. 若3，a，4，5的众数是4，则这组数据的平均数是.

查看试题解析
8. 若 $\frac{x}{2} = \frac{y}{3} = \frac{z}{4}$ ，则 $\frac{x + y + z}{x} =$ .

查看试题解析
9. 已知圆锥的底面半径为3，侧面积为15π，则这个圆锥的母线长为.

查看试题解析
10. 如图，已知∠A=∠D，要使△ABC∽△DEF，还需添加一个条件，你添加的条件是.（只需写一个条件，不添加辅助线和字母）

查看试题解析
11. 若点A(2，m)在函数 $y = x^{2} - 1$ 的图象上，则点A关于 $x$ 轴的对称点的坐标是.

查看试题解析
12. 抛物线y=（x-1）²-7的对称轴为直线.

查看试题解析
13. 如图，二次函数y＝ax²+bx+3的图象经过点A（﹣1，0），B（3，0），那么一元二次方程ax²+bx＝0的根是.

查看试题解析
14. 已知x₁ ， x₂ ， x₃ ， x₄的方差是2，则3x₁﹣2，3x₂﹣2，3x₃﹣2，3x₄﹣2的方差是.

查看试题解析
15. 如图，在Rt△AOB中，OA=OB= $3 \sqrt{2}$ ，⊙O的半径为1，点P是AB边上的动点，过点P作⊙O的一条切线PQ（点Q为切点），则切线PQ的最小值为.

查看试题解析
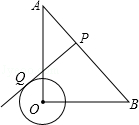16. 在矩形ABCD中，∠B的平分线BE与AD交于点E，∠BED的平分线EF与DC交于点F，若AB=9，DF=2FC，则BC=.（结果保留根号）

查看试题解析

三、解答题

17. 解方程: $x^{2} - 3 x = 0$

查看试题解析
18. 一只箱子里共有3个球，其中2个白球，1个红球，它们除颜色外均相同。

(1)、从箱子中任意摸出一个球是白球的概率是多少？

(2)、从箱子中任意摸出一个球，不将它放回箱子，搅匀后再摸出一个球，求两次摸出球的都是白球的概率，并画出树状图。

查看试题解析
19. 如图，在半径为13的⊙O中，OC垂直弦AB于点D，交⊙O于点C，AB=24，求CD的长.

查看试题解析
20. 如图.在□ABCD中，点E在边BC上，点F在边AD的延长线上，且DF=BE.EF与CD交于点G.若 $\frac{D G}{G C} = \frac{2}{3}$ ，BE=4，求BC的长.

查看试题解析
21. 如图，△ABC中，∠B=45°，AB=3 $\sqrt{2}$ ，D是BC中点，tanC= $\frac{1}{5}$ .

求：

(1)、BC的长；

(2)、sin∠ADB.

查看试题解析
22. 如图，AB是半圆O的直径，点P是BA延长线上一点，PC是⊙O的切线，切点为C，过点B作BD⊥PC交PC的延长线于点D，连接BC.求证：

(1)、∠PBC=∠CBD；

(2)、 $B C^{2}$ =AB•BD.

查看试题解析
23. 已知二次函数y=x²+2x+m的图象C₁与x轴有且只有一个公共点.

(1)、求C₁的顶点坐标；

(2)、将C₁向下平移若干个单位后，得抛物线C₂ ，如果C₂与x轴的一个交点为A（—3，0），求C₂的函数关系式，并求C₂与x轴的另一个交点坐标；

查看试题解析
24. 如图，点B、D、E在一条直线上，BE与AC相交于点F，且 $\frac{A B}{A D} = \frac{B C}{D E} = \frac{A C}{A E}$

(1)、求证：△ABC∽△ADE；

(2)、求证：∠BAD=∠CAE；

(3)、若∠BAD=18°，求∠EBC的度数.

查看试题解析
25. 某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试销．据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件，但要求销售单价不得低于成本．

(1)、求出每天的销售利润y（元）与销售单价x（元）之间的函数关系式；

(2)、求出销售单价为多少元时，每天的销售利润最大？最大利润是多少？

(3)、如果该企业要使每天的销售利润不低于4000元，且每天的总成本不超过7000元，那么销售单价应控制在什么范围内？（每天的总成本=每件的成本×每天的销售量）

查看试题解析
26. 如图，直线 $l$ 与⊙ $O$ 相切于点 $A ， A C$ 为⊙ $O$ 的直径， $A C = 8 ， P$ 是直径 $A C$ 右侧半圆上的一个动点(不与点 $A$ 、 $C$ 重合)，过点 $P$ 作 $P B ⊥ l$ ，垂足为 $B$ ，连接 $P A$ 、 $P C$ .设 $P A = x$ ， $P B = y$ .

求：

(1)、 $Δ A P C$ 与 $Δ A P B$ 相似吗?为什么?

(2)、求 $y$ 与 $x$ 的函数关系式；

(3)、当 $x$ 为何值时， $x - y$ 取得最大值，最大值为多少?

查看试题解析
27.
如图，已知抛物线经过原点O，顶点为A（1，1），且与直线y=x﹣2交于B，C两点．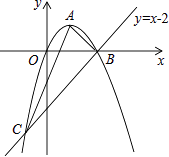

(1)、求抛物线的解析式及点C的坐标；

(2)、求证：△ABC是直角三角形；

(3)、若点N为x轴上的一个动点，过点N作MN⊥x轴与抛物线交于点M，则是否存在以O，M，N为顶点的三角形与△ABC相似？若存在，请求出点N的坐标；若不存在，请说明理由．

查看试题解析