江苏省宝应县东北片六校2019届九年级上学期数学第二次联考试卷
试卷更新日期:2019-09-30 类型:月考试卷
一、单选题
-
1. 方程 的根是( )A、 B、x=0 C、 , D、 ,2. 一组数据1,2,3,0,-2,-3的极差是( )A、6 B、5 C、4 D、33. 在Rt△ABC中,∠C=90°,AB=13,AC=5,则sinA的值为( )
A、 B、 C、 D、4. 一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根5. 对于二次函数 y=(x﹣1)2+2 的图象,下列说法正确的是( )A、开口向下 B、顶点坐标是(﹣1,2) C、对称轴是 x=1 D、与 x 轴有两个交点6. 某商品经过连续两次降价,销售单价由原来100元降到81元 设平均每次降价的百分率为x,根据题意可列方程为( )A、 B、 C、 D、7. 下列问题中,错误的个数是( )( 1 )三点确定一个圆;(2)平分弦的直径垂直于弦;(3)相等的圆心角所对的弧相等;(4)正五边形是轴对称图形.
A、1个 B、2个 C、3个 D、4个8. 二次函数y=ax²+bx+2(a≠0)的图像经过点(-1,1)则代数1-a+b的值为( )A、-3 B、-1 C、2 D、59. AB为半圆O的直径,现将一块等腰直角三角板如图放置,锐角顶点P在半圆上,斜边过点B,一条直角边交该半圆于点Q.若AB=2,则线段BQ的长为多少?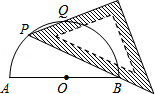 10. 如图,抛物线y=ax2+bx+c交x轴于(﹣1,0)、(3,0)两点,以下四个结论正确的是(用序号表示).
10. 如图,抛物线y=ax2+bx+c交x轴于(﹣1,0)、(3,0)两点,以下四个结论正确的是(用序号表示).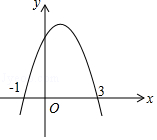
( 1 )图象的对称轴是直线x=1(2)当x>1时,y随x的增大而减小(3)一元二次方程ax2+bx+c=0的两个根是﹣1和3(4)当﹣1<x<3时,y<0.
二、填空题
-
11. 抛物线 的顶点坐标是.12. “植树节”时,九(1)班6个小组的植树棵数分别是:5,7,3,x,6,4.已知这组数据的众数是5,则该组数据的平均数是13. 甲、乙两人5次射击命中的环数分别为,甲:7,9,8,6,10;乙:7,8,9,8,8; =8,则这两人5次射击命中的环数的方差S甲2S乙2(填“>”“<”或“=”).14. 正方形的边长为2,则它的内切圆与外接圆围成的圆环面积为.15. 设m,n分别为一元二次方程x2+2x﹣2018=0的两个实数根,则m2+3m+n= .16. 如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是.
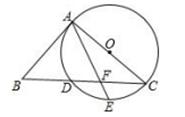
 17. 如图,AB为☉O的切线,切点为B,连接AO,AO与☉O交于点C,BD为☉O的直径,连接CD.若∠A=30°,☉O的半径为2,则图中阴影部分的面积为.
17. 如图,AB为☉O的切线,切点为B,连接AO,AO与☉O交于点C,BD为☉O的直径,连接CD.若∠A=30°,☉O的半径为2,则图中阴影部分的面积为. 18. 如图,在扇形铁皮AOB中,OA=10,∠AOB=36°,OB在直线l上.将此扇形沿l按顺时针方向旋转(旋转过程中无滑动),当OA第5次落在l上时,停止旋转.则点O所经过的路线长为.
18. 如图,在扇形铁皮AOB中,OA=10,∠AOB=36°,OB在直线l上.将此扇形沿l按顺时针方向旋转(旋转过程中无滑动),当OA第5次落在l上时,停止旋转.则点O所经过的路线长为.
三、解答题
-
19. 计算:(1)、 cos30°+ sin45°(2)、2cos45°+ -20. 解方程:(1)、(2)、21. 一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.(1)、从中任意摸出1个球,恰好摸到红球的概率是;(2)、先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.22. 已知关于 的一元二次方程(1)、若方程的一个根为 ,求 的值及另一个根;(2)、若该方程根的判别式的值等于 ,求 的值.23. 如图, 和 是直立在地面上的两根立柱,已知 ,某一时刻 在太阳光下的影子长 .
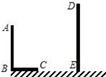 (1)、在图中画出此时 在太阳光下的影子 ;(2)、在测量 的影子长时,同时测量出 ,计算 的长.24. 已知二次函数y=﹣x2+2x.
(1)、在图中画出此时 在太阳光下的影子 ;(2)、在测量 的影子长时,同时测量出 ,计算 的长.24. 已知二次函数y=﹣x2+2x. (1)、在给定的平面直角坐标系中,画出这个函数的图象;(2)、根据图象,写出当y<0时,x的取值范围;(3)、若将此图象沿x轴向左平移3个单位,再沿y轴向下平移1个单位,请直接写出平移后图象所对应的函数关系式.25. 某商品交易会上,一商人将每件进价为5元的纪念品,按每件9元出售,每天可售出32件.他想采用提高售价的办法来增加利润,经试验,发现这种纪念品每件提价2元,每天的销售量会减少8件.(1)、当售价定为多少元时,每天的利润为140元?(2)、写出每天所得的利润y(元)与售价 (元/件)之间的函数关系式,每件售价定为多少元,才能使一天所得的利润最大?最大利润是多少元?(利润=(售价-进价)×售出件数)
(1)、在给定的平面直角坐标系中,画出这个函数的图象;(2)、根据图象,写出当y<0时,x的取值范围;(3)、若将此图象沿x轴向左平移3个单位,再沿y轴向下平移1个单位,请直接写出平移后图象所对应的函数关系式.25. 某商品交易会上,一商人将每件进价为5元的纪念品,按每件9元出售,每天可售出32件.他想采用提高售价的办法来增加利润,经试验,发现这种纪念品每件提价2元,每天的销售量会减少8件.(1)、当售价定为多少元时,每天的利润为140元?(2)、写出每天所得的利润y(元)与售价 (元/件)之间的函数关系式,每件售价定为多少元,才能使一天所得的利润最大?最大利润是多少元?(利润=(售价-进价)×售出件数)