湖北省武汉市硚口区2019届九年级上学期数学12月月考试卷
试卷更新日期：2019-09-30 类型：月考试卷
一、单选题
-
1. 平面直角坐标系中，点A(－1，2)关于原点的对称点是（ ）A、(1，2) B、(1，－2) C、(－1，－2) D、(－1，2)2. 抛物线y＝(x－2)2－3的对称轴是（ ）A、y轴 B、直线x＝2 C、直线x＝－2 D、直线x＝－33. 已知⊙O的半径是4，OP＝3，则点P与⊙O的位置关系是（ ）A、点P在⊙O外 B、点P在⊙O上 C、点P在⊙O内 D、不能确定4. 如图，⊙O中，弦AB、CD相交于点P，∠A＝40°，∠APD＝75°，则∠B的度数是（ ）
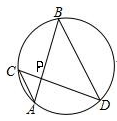A、15° B、40° C、75° D、35°5. 如图，下列条件使△ACD∽△ABC成立的是（ ）
A、 B、 C、AC2＝AD·AB D、CD2＝AD·BD6. 如图，EF为⊙O的直径，弦CD⊥EF于M.已知CD＝6，EM＝9，则⊙O的半径为（ ）
A、4 B、5 C、6 D、87. 如图，Rt△ABC中，∠C＝90°，AB＝13，BC＝5，则其内切圆半径为（ ）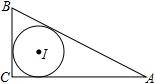
A、1 B、2 C、3 D、48. 如图，在平行四边形ABCD中，EF∥AB交AD于E，交BD于F，DE：EA=3：4，EF=3，则CD的长为（ ）
A、4 B、7 C、3 D、129. 如图，正方形的边长为a，以各边为直径在正方形内作半圆，则圆中阴影部分的面积为（ ）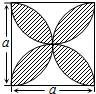
A、πa2－a2 B、 πa2－a2 C、 πa2－ a2 D、2πa2－a210. 如图，在等腰Rt△ABC中，AC＝BC＝2 ，点P在以斜边AB为直径的半圆上，M为PC的中点.当点P沿半圆从点A运动至点B时，点M运动的路径长是（ ）
A、2 B、2 C、π D、 π二、填空题
-
11. 若正六边形的边长是4，则其半径是 ， 边心距是 ， 面积是12. 用一个圆心角为120°，半径为4的扇形作一个圆锥的侧面，这个圆锥的底面圆的半径为 ．13. 如图，AB是半圆的直径，点D是弧AC的中点，∠ABC＝50°，则∠DAB的度数是.
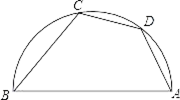14. 如图，在正方形ABCD中，AD＝1.将△ABD绕点B顺时针旋转45°得到△A′BD′，此时AD与CD交于点E，则DE的长度为
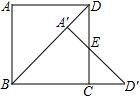15. 如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于D点.若 ，则 ＝
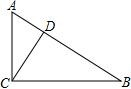16. 在△ABC中，AB＝AC，点O是△ABC的外心，∠BOC＝60°，BC＝2，则S△ABC＝。三、解答题
-
17. 解方程：x2﹣5x+3=0．18. 如图，⊙O的弦AB和弦CD相交于点E，AB＝CD，求证：AD＝CB
19. 如图，点C、D在线段AB上，△PCD是等边三角形，∠APB＝120°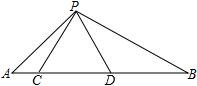
(1)、求证：△ACP∽△PDB(2)、若PC＝3，AC＝1，求BD的长20. 如图，点E是△ABC的内心，AE的延长线和△ABC的外接圆相交于点D，连接BE
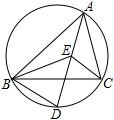(1)、若∠CBD＝35°，求∠BAC及∠BEC的度数(2)、求证：DE＝DB21. 如图，PA为⊙O的切线，A为切点，过A作弦AB⊥OP，垂足为点C，延长BO与PA的延长线交于点D
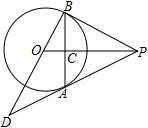(1)、求证：PB为⊙O的切线(2)、若OB＝3，OD＝5，求PB的长22. 如图，锐角△ABC中，BC＝12，BC边上的高AD＝8，矩形EFGH的边GH在BC上，其余两点E、F分别在AB、AC上，且EF交AD于点K
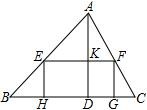(1)、求 的值(2)、设EH＝x，矩形EFGH的面积为S①求S与x的函数关系式
②请直接写出S的最大值
23. 如图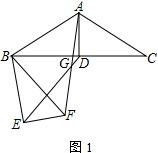
(1)、如图，AD是等腰△ABC的中线，AB＝AC.把△BDA绕B点顺时针旋转α角度（0°＜α＜90°）得到△BEF，点D对应E点，点A对应F点，AF与DE交于点G。①求证：△BAF∽△BDE
②求证：AG＝FG
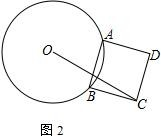
(2)、如图，AB是⊙O的一条运动的弦，以AB为边向圆外作正方形ABCD.若⊙O的半径为2，则OC的长的最大值是.24. 抛物线y＝ax2＋bx＋3经过点(2，－1)，与x轴交于A(1，0)、B两点，与y轴交于点C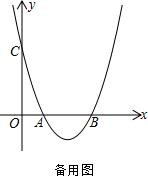
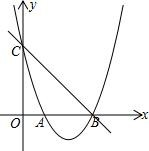(1)、求抛物线解析式(2)、如图，点E是直线BC下方抛物线上的一动点.当△BEC面积最大时，请求出点E的坐标(3)、点P是第四象限内抛物线上的一动点，PA交y轴于D，BP交y轴于E，过P作PN⊥y轴于N，求 的值