湖北省武汉市蔡甸区八校2019届九年级上学期数学12月月考试卷

试卷更新日期：2019-09-30 类型：月考试卷

进入 出卷网 下载

一、单选题

  • 1. 下列图形中，即是中心对称图形，又是轴对称图形的是（   ）
    A、 B、 C、 D、

    查看试题解析

  • 2. 用配方法解方程x2－4x＋1＝0，变形正确的是（   ）
    A、(x＋2)2＝5 B、(x－2)2＝5 C、(x＋2)2＝3 D、(x－2)2＝3

    查看试题解析

  • 3. 自行车车轮要做成圆形，主要是根据圆的以下哪个特征（   ）
    A、圆是轴对称图形 B、圆是中心对称图形 C、圆上各点到圆心的距离相等 D、直径是圆中最长的弦

    查看试题解析

  • 4. 关于函数y＝－(x＋2)2－1的图象叙述正确的是（   ）
    A、开口向上 B、顶点(2，－1) C、与y轴交点为(0，－1) D、图象都在x轴下方

    查看试题解析

  • 5. 某企业2018年年利润为300万元，计划2020年年利润为507万元.设这两年的年利润平均增长率为x.应列方程是（   ）
    A、300(1＋x)＝507 B、300(1＋x)2＝507 C、300(1＋x)＋3(1＋x)2＝507 D、300＋300(1＋x)＋3(1＋x)2＝507.

    查看试题解析

  • 6. 如表中列出了二次函数y＝ax2＋bx＋c的x、y的一些对应值，则一元二次方程ax2＋bx＋c＝0的一个解x1的范围是（   ）

    x

    …

    －3

    －2

    －1

    0

    1

    …

    y

    …

    －11

    －5

    －1

    1

    1

    …
    A、－3＜x1＜－2 B、－2＜x1＜－1 C、－1＜x1＜0 D、0＜x1＜1.

    查看试题解析

  • 7. 如图，将△ABC绕点C顺时针旋转90°得到△EDC ． 若点A ， D ， E在同一条直线上，∠ACB=20°，则∠ADC的度数是（ ）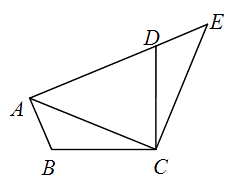

    A、55° B、60° C、65° D、70°

    查看试题解析

  • 8. 已知x1、x2是关于x的方程x2－ax－1＝0的两个实数根，下列结论一定正确的是（   ）
    A、x1≠x2 B、x1＋x2＞0 C、x1×x2＞0 D、1x1 ＋ 1x2 ＞0

    查看试题解析

  • 9. 如图，AB是⊙O的直径，点C，D，E在⊙O上，若∠AED=20°，则∠BCD的度数为（   ）

    A、100° B、110° C、115° D、120°

    查看试题解析

  • 10. 如图，二次函数y=ax2+bx+c的图像经过点A（-1，0），点B（3，0），交y轴正半轴于点C，给出下列结论：①a＝－1，b＝2，c＝3；②若0＜x＜4，则5a＜y＜－3a；③对任意实数m，一定有am2＋bm＋a≤0；④一元二次方程cx2＋bx＋a＝0的两个根为－1和 13 .其中正确的结论是（ ）

    A、①③ B、②③ C、②④ D、③④

    查看试题解析

  • 11. 在平面直角坐标系中，点A(－3，2)关于原点对称的点的坐标为.

    查看试题解析

二、填空题

  • 12. 方程x(x－1)＝0的根是.

    查看试题解析

  • 13. 已知关于x的一元二次方程(k＋1)x2－2x＋1＝0有实数根，则k的取值范围是.

    查看试题解析

  • 14. 已知在△ABC中，AB=CB，以AB为直径的⊙O交于点D，过D作⊙O的切线交AC于E，且DE⊥AC，则∠C的度数为＝.

    查看试题解析

  • 15. 某架飞机着陆后滑行的距离y(单位：m)关于滑行时间t(单位：s)的函数解析式是y＝60t－ 32 t2 ， 这架飞机着陆后滑行最后150m所用的时间是s.

    查看试题解析

  • 16. 如图，点C是半圆 AB⌢ 上一动点，以BC为边作正方形BCDE，使 BC⌢ 在正方形内，连OE，若AB=4cm，则OD的最大值为cm.

    查看试题解析

三、解答题

  • 17. 求抛物线y＝x2－2x＋1与x轴的交点坐标.

    查看试题解析

  • 18. 如图，在△OAB中OA＝OB，⊙O交AB于点C、D，求证：AC＝BD.

    查看试题解析

  • 19. 如图，△ABC三个顶点为A(3，4)、B(5，4)、C(1，2).请解答下列问题：

    (1)、①画出△ABC关于y轴对称的△A1B1C1 ， 使点A1与A对应，点B1与B对应；

    ②画出△ABC绕点O顺时针旋转90°后得到的△A2B2C2 ， 使点A2与A对应，点B2与B对应；

    (2)、若△A1B1C1和△A2B2C2关于某直线对称，请直接写出该直线的解析式；
    (3)、直接写出△ABC的外心坐标.

    查看试题解析

  • 20. 如图，半圆O的直径为AB，D是半圆上的一个动点（不与点A，B重合），连接BD并延长至点C，使CD＝BD，连接AC，过点D作DE⊥AC于点E.

    (1)、请猜想DE与⊙O的位置关系，并说明理由；
    (2)、当AB＝4，∠BAC＝45°时，求DE的长.

    查看试题解析

  • 21. 如图，已知抛物线L1：y= 12 x2－x－ 32 ，L1交x轴于A，B（点A在点B左边），交y轴于C，其顶点为D，P是L1上一个动点，过P沿y轴正方向作线段PQ∥y轴，使PQ=t，当P点在L1上运动时，Q随之运动形成的图形记为L2.

    (1)、若t=3，求图形L2的函数解析式；
    (2)、过B作直线l∥y轴，若直线l和y轴及L1 ， L2所围成的图形面积为12，求t的值.

    查看试题解析

  • 22. 如图，某工程队在工地互相垂直的两面墙AE、AF处，用180米长的铁栅栏围成一个长方形场地ABCD，中间用同样材料分割成两个长方形.已知墙AE长120米，墙AF长40米，要使长方形ABCD的面积为4000平方米，问BC和CD各取多少米？

    查看试题解析

  • 23. 已知△ABC为等边三角形，P是直线AC上一点，AD⊥BP于D，以AD为边作等边△ADE（D，E在直线AC异侧）.

    (1)、如图1，若点P在边AC上，连CD，且∠BDC=150°，则 ADBD =；（直接写结果）
    (2)、如图2，若点P在AC延长线上，DE交BC于F求证：BF=CF；
    (3)、在图2中，若∠PBC=15°，AB= 6+2 ，请直接写出CP的长.

    查看试题解析

  • 24. 已知二次函数y=ax2+bx+c的图象对称轴为x= 12 ，图象交x轴于A，B，交y轴于C（0，-3），且AB=5，直线y=kx+b（k＞0）与二次函数图象交于M，N（M在N的右边），交y轴于P.

    (1)、求二次函数图象的解析式；
    (2)、若b=-5，且△CMN的面积为3，求k的值；
    (3)、若b=-3k，直线AN交y轴于Q，求 CPCQ 的值或取值范围.

    查看试题解析