江苏省东台市第七联盟2019届九年级上学期数学12月月考试卷
试卷更新日期:2019-09-30 类型:月考试卷
一、单选题
-
1. 抛物线y=2(x-3)2-1的顶点坐标是( )A、(3,1) B、(3,-1) C、(-3,1) D、(-3,-1)2. Rt△ABC中,∠C=90°,a=4,b=3,则cosA的值是( )A、 B、 C、 D、3. 如图,已知a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F,若 = ,则 的值是( )
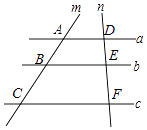 A、 B、 C、 D、14. 如图,若A,B,C,P,Q,甲、乙、丙、丁都是方格纸中的格点,为使△ABC∽△PQR,则点R应是甲、乙、丙、丁四点中的( )
A、 B、 C、 D、14. 如图,若A,B,C,P,Q,甲、乙、丙、丁都是方格纸中的格点,为使△ABC∽△PQR,则点R应是甲、乙、丙、丁四点中的( ) A、甲 B、乙 C、丙 D、丁5. 如图,在□ABCD中,点E是边AD的中点,EC交对角线BD于点F,则DF:FB等于 ( )
A、甲 B、乙 C、丙 D、丁5. 如图,在□ABCD中,点E是边AD的中点,EC交对角线BD于点F,则DF:FB等于 ( ) A、1∶1 B、1∶2 C、1∶3 D、2∶36. 在同一时刻太阳光线是平行的,如果高1.5米的测杆影长3米,那么此时影长36米的旗杆的高度为( )A、18米 B、12米 C、15米 D、20米7. 二次函数 的图象经过点(-1,1),则代数式 的值为( )A、-3 B、-1 C、2 D、58. 抛物线y=ax2+bx+c(a≠0)图象如图所示,下列结论错误的是( )
A、1∶1 B、1∶2 C、1∶3 D、2∶36. 在同一时刻太阳光线是平行的,如果高1.5米的测杆影长3米,那么此时影长36米的旗杆的高度为( )A、18米 B、12米 C、15米 D、20米7. 二次函数 的图象经过点(-1,1),则代数式 的值为( )A、-3 B、-1 C、2 D、58. 抛物线y=ax2+bx+c(a≠0)图象如图所示,下列结论错误的是( )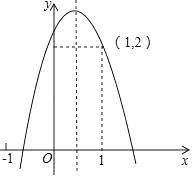 A、abc<0 B、a+c<b C、b2+8a>4ac D、2a+b>0
A、abc<0 B、a+c<b C、b2+8a>4ac D、2a+b>0二、填空题
-
9. 如果 ,那么 = .10. 如图,△ABC中,∠BAC=90°,点G是△ABC的重心,如果AG=4,那么BC=.
 11. 已知线段MN=6cm,P是线段MN的一个黄金分割点,则其中较长线段MP的长是.12. 在△ABC中,若|cosA- |+(1-tanB)2=0,则∠C的度数是.
11. 已知线段MN=6cm,P是线段MN的一个黄金分割点,则其中较长线段MP的长是.12. 在△ABC中,若|cosA- |+(1-tanB)2=0,则∠C的度数是.
13. 如图所示,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12米,塔影长DE=18米,小明和小华的身高都是1.6米,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2米和1米,那么塔高AB为米。 14. 已知D是等边△ABC边AB上的一点,现将△ABC折叠,使点C与D重合,折痕为EF,点E、F分别在AC和BC上.如图,若AD∶DB=1∶4,则CE∶CF=.
14. 已知D是等边△ABC边AB上的一点,现将△ABC折叠,使点C与D重合,折痕为EF,点E、F分别在AC和BC上.如图,若AD∶DB=1∶4,则CE∶CF=.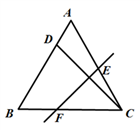 15. 如图,⊙O是等边三角形 的外接圆, 是⊙O上的一个点, 是 延长线上的一个点,且∠ =∠ ,若 , ,则线段 的长是.
15. 如图,⊙O是等边三角形 的外接圆, 是⊙O上的一个点, 是 延长线上的一个点,且∠ =∠ ,若 , ,则线段 的长是. 16. 方格纸中每个小正方形的边长都是单位1,△OAB在平面直角坐标系中的位置如图所示.解答问题:
16. 方格纸中每个小正方形的边长都是单位1,△OAB在平面直角坐标系中的位置如图所示.解答问题: (1)、请按要求对△ABO作如下变换:
(1)、请按要求对△ABO作如下变换:①将△OAB向下平移2个单位,再向左平移3个单位得到△O1A1B1;
②以点O为位似中心,位似比为2:1,将△ABC在位似中心的异侧进行放大得到△OA2B2.
(2)、写出点A1 , A2的坐标: , ;(3)、△OA2B2的面积为.三、解答题
-
17.(1)、计算:- tan60°+4sin30°×cos245°(2)、用配方法解方程:x2﹣2x﹣1=018. 射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次
第二次
第三次
第四次
第五次
第六次
平均成绩
中位数
甲
10
8
9
8
10
9
9
①
乙
10
7
10
10
9
8
②
9.5
(1)、完成表中填空①;②;(2)、请计算甲六次测试成绩的方差;(3)、若乙六次测试成绩方差为 ,你认为推荐谁参加比赛更合适,请说明理由.19. 小颖和小丽做“摸球”游戏:在一个不透明的袋子中装有编号为1~4的四个球(除编号外都相同),从中随机摸出一个球,记下数字后放回,再从中摸出一个球,记下数字。若两次数字之和大于5,则小颖胜,否则小丽胜。这个游戏对双方公平吗?请说明理由。20. 如图,△ABC中,∠A=30°,∠B=45°,AC=4,求AB的长. 21. 如图,操场上有一根旗杆AH.为测量它的高度,在B和D处各立一根高1.5米的标杆BC、DE,两杆相距30米,测得视线AC与地面的交点为F,视线AE与地面的交点为G,并且H、B、F、D、G都在同一直线上,测得BF为3米,DG为5米,求旗杆AH的高度?
21. 如图,操场上有一根旗杆AH.为测量它的高度,在B和D处各立一根高1.5米的标杆BC、DE,两杆相距30米,测得视线AC与地面的交点为F,视线AE与地面的交点为G,并且H、B、F、D、G都在同一直线上,测得BF为3米,DG为5米,求旗杆AH的高度? 22. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
22. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F. (1)、求证:DF⊥AC;(2)、若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.23. 由于雾霾天气对人们健康的影响,市场上的空气净化器成了热销产品.某公司经销一种空气净化器,每台净化器的成本价为200元.经过一段时间的销售发现,每月的销售量y(台)与销售单价x(元)的关系为y=﹣2x+1000.(1)、该公司每月的利润为w元,写出利润w与销售单价x的函数关系式;(2)、若要使每月的利润为40000元,销售单价应定为多少元?(3)、公司要求销售单价不低于250元,也不高于400元,求该公司每月的最高利润和最低利润分别为多少?24. 如图,在Rt△ABC中,∠ACB=90°,以BC为半径作⊙B,交AB于点D,交AB的延长线于点E,连接CD、CE.
(1)、求证:DF⊥AC;(2)、若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.23. 由于雾霾天气对人们健康的影响,市场上的空气净化器成了热销产品.某公司经销一种空气净化器,每台净化器的成本价为200元.经过一段时间的销售发现,每月的销售量y(台)与销售单价x(元)的关系为y=﹣2x+1000.(1)、该公司每月的利润为w元,写出利润w与销售单价x的函数关系式;(2)、若要使每月的利润为40000元,销售单价应定为多少元?(3)、公司要求销售单价不低于250元,也不高于400元,求该公司每月的最高利润和最低利润分别为多少?24. 如图,在Rt△ABC中,∠ACB=90°,以BC为半径作⊙B,交AB于点D,交AB的延长线于点E,连接CD、CE. (1)、求证:△ACD∽△AEC;(2)、当 时,求tanE;(3)、若AD=4,AC=4 ,求△ACE的面积.25. 阅读与应用:
(1)、求证:△ACD∽△AEC;(2)、当 时,求tanE;(3)、若AD=4,AC=4 ,求△ACE的面积.25. 阅读与应用:阅读1:a、b为实数,且a>0,b>0,因为 ,所以 ,从而 (当a=b时取等号).
阅读2:函数 (常数m>0,x>0),由阅读1结论可知: ,所以当 即 时,函数 的最小值为 .
阅读理解上述内容,解答下列问题:
(1)、问题1:已知一个矩形的面积为4,其中一边长为x,则另一边长为 ,周长为 ,求当x=时,周长的最小值为 .
(2)、问题2:已知函数y1=x+1(x>-1)与函数y2=x2+2x+17(x>-1),当x=时, 的最小值为 .
(3)、问题3:某民办学习每天的支出总费用包含以下三个部分:一是教职工工资6400元;二是学生生活费每人10元;三是其他费用.其中,其他费用与学生人数的平方成正比,比例系数为0.01.当学校学生人数为多少时,该校每天生均投入最低?最低费用是多少元?(生均投入=支出总费用÷学生人数)
26. 已知:如图1,直线 与x轴、y轴分别交于点A、C两点,点B的横坐标为2. (1)、求A、C两点的坐标和抛物线的函数关系式;(2)、点D是直线AC上方抛物线上任意一点,P为线段AC上一点,且S△PCD=2S△PAD ,求点P的坐标;(3)、如图2,另有一条直线y=-x与直线AC交于点M,N为线段OA上一点,∠AMN=∠AOM.点Q为x轴负半轴上一点,且点Q到直线MN和直线MO的距离相等,求点Q的坐标.
(1)、求A、C两点的坐标和抛物线的函数关系式;(2)、点D是直线AC上方抛物线上任意一点,P为线段AC上一点,且S△PCD=2S△PAD ,求点P的坐标;(3)、如图2,另有一条直线y=-x与直线AC交于点M,N为线段OA上一点,∠AMN=∠AOM.点Q为x轴负半轴上一点,且点Q到直线MN和直线MO的距离相等,求点Q的坐标.