江苏省镇江市句容市2019届九年级上学期数学10月月考试卷

试卷更新日期：2019-09-30 类型：月考试卷

进入出卷网下载

一、单选题

1. 一元二次方程 $y^{2} - y - \frac{3}{4} = 0$ 配方后可化为（）

A、 ${(y + \frac{1}{2})}^{2} = 1$ B、 ${(y - \frac{1}{2})}^{2} = 1$ C、 ${(y + \frac{1}{2})}^{2} = \frac{3}{4}$ D、 ${(y - \frac{1}{2})}^{2} = \frac{3}{4}$

查看试题解析
2. 八年级（2）班学生积极参加献爱心活动，该班50名学生的捐款情况统计如表，则该班学生捐款金额的平均数和中位数分别是（）

金额/元

5

10

20

50

100

人数

4

16

15

9

6

A、20.6元和10元 B、20.6元和20元 C、30.6元和10元 D、30.6元和20元

查看试题解析
3. 已知α、β是方程x²﹣2x﹣4＝0的两个实数根，则α³+8β+6的值为（）

A、﹣1 B、2 C、22 D、30

查看试题解析
4. 在纸上剪下一个圆形和一个扇形纸片，使之恰好能够围成一个圆锥模型，若圆的半径为r，扇形的半径为R，扇形的圆心角等于120°（如图），则r与R之间的关系是（）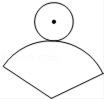

A、R=2r B、R= $\sqrt{3}$ r C、R=3r D、R=4r

查看试题解析
5. 如图，点A，B，C均在坐标轴上，AO=BO=CO=1，过A，O，C作⊙D，E是⊙D上任意一点，连结CE， BE，则 $C E^{2} + B E^{2}$ 的最大值是（）

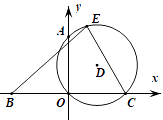A、4 B、5 C、6 D、 $4 + \sqrt{2}$

查看试题解析

二、填空题

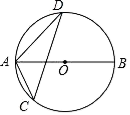
6. 方程x²－5x＝0的解是.

查看试题解析
7. 下列方程中，①x²=0；②x²=y+4；③ax²+2x﹣3=0（其中a是常数）；④x（2x﹣3）=2x（x﹣1）；⑤ $\frac{1}{2}$ （x²+3）= $\sqrt{3}$ x，一定是一元二次方程的有（填序号）.

查看试题解析
8. 已知a是方程x²﹣2018x+1=0的一个根a，则a²﹣2017a+ $\frac{2018}{a^{2} + 1}$ 的值为.

查看试题解析
9. 若关于x的一元二次方程 $\frac{1}{2}$ x²﹣2mx﹣4m+1=0有两个相等的实数根，则（m﹣2）²﹣2m（m﹣1）的值为.

查看试题解析
10. 若一组数据6、7、4、6、x、1的平均数是5，则这组数据的众数是.

查看试题解析
11. 一组数据2，x，4，3，3的平均数是3，则这组数据的中位数是．

查看试题解析
12. 如图，AB为⊙O的直径，CD为⊙O的弦，∠ACD＝54°，则∠BAD＝.

查看试题解析
13. 如图，点E是正方形ABCD的边CD上一点，以A为圆心，AB为半径的弧与BE交于点F，则∠EFD＝°.

查看试题解析
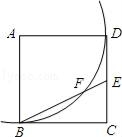14. 如图，扇形纸扇完全打开后，∠BAC=120°，AB=AC=30厘米，则 $\overset{⏜}{B C}$ 的长为厘米.（结果保留π）

查看试题解析
15. 如图，正六边形ABCDEF的边长为1，以点A为圆心，AB的长为半径，作扇形ABF，则图中阴影部分的面积为 (结果保留根号和 $π$ )．

查看试题解析
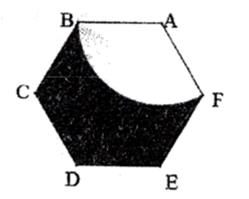16. 在△ABC中，∠C=90°，AB=5，BC=4，以A为圆心，3为半径作圆，则点C与圆A的位置关系为：点C在圆A.

查看试题解析
17. 若β（β≠0）是关于x的方程ax²+bx+c=0（a≠0）的根，则以 $\frac{1}{β}$ 为根的一元二次方程为.

查看试题解析

三、解答题

18.

(1)、用配方法解方程： $3 x^{2} - 12 x + 9 = 0$ .

(2)、用公式法解方程： $3 x^{2} - 9 x + 4 = 0$ .

查看试题解析
19. 为了参加“荆州市中小学生首届诗词大会”，某校八年级的两班学生进行了预选，其中班上前5名学生的成绩（百分制）分别为：八（1）班86，85，77，92，85；八（2）班79，85，92，85，89．通过数据分析，列表如下：
班级
平均分
中位数
众数
方差
八（1）
85
b
c
22.8
八（2）
a
85
85
19.2

(1)、直接写出表中a，b，c的值；

(2)、根据以上数据分析，你认为哪个班前5名同学的成绩较好？说明理由．

查看试题解析
20. 如图，A，B，C三点在⊙O上，直径BD平分∠ABC，过点D作DE∥AB交弦BC于点E，过点D作⊙O的切线交BC的延长线于点F.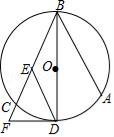

(1)、求证：EF=ED；

(2)、如果半径为5，cos∠ABC= $\frac{3}{5}$ ，求DF的长.

查看试题解析
21. 已知：关于x的一元二次方程kx²﹣（4k+1）x+3k+3＝0（k是整数）．

(1)、求证：方程有两个不相等的实数根；

(2)、若方程的两个实数根都是整数，求k的值．

查看试题解析
22.

(1)、解方程：2x²+x﹣6=0；

(2)、阅读理解：为解方程（x²﹣1）²﹣5（x²﹣1）+4=0，我们可以将x²﹣1视为一个整体，然后设x²﹣1=y，则原方程化为y²﹣5y+4=0，解此方程得：y₁=1，y₂=4．当y=1时，x²﹣1=1，x=± $\sqrt{2}$ ；当y=4时，x²﹣1=4，∴x=± $\sqrt{5}$
∴原方程的解为：x₁= $\sqrt{2}$ ，x₂=﹣ $\sqrt{2}$ ，x₂= $\sqrt{5}$ ，x₁=﹣ $\sqrt{5}$

以上方法叫做换元法解方程，达到了降次的目的，体现了转化思想．

运用上述方法解方程：x⁴﹣8x²+12=0．

查看试题解析
23. 铜陵市义安区实施了城乡居民基本医疗保险（简称“医疗保险”），办法规定农村村民只要每人每年交纳180元钱就可以加入医疗保险，住院时自己先垫付，出院同时就可得到按一定比例的报销款，这项举措惠及民生，吴斌与同学随机调查了他们镇的一些农民，根据收集到的数据绘制了以下的统计图.
根据图中信息，解答下列问题：

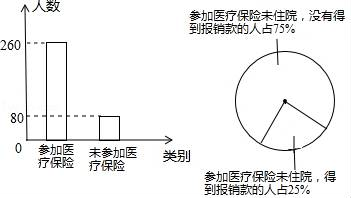(1)、本次调查了多少村民？被调查的村民中参加医疗保险，得到报销款的有多少人？

(2)、若该镇有34000村民，请估算有多少人参加了医疗保险？要使两年后参加医疗保险的人数增加到业务31460人，假设这两年的年增长率相同，求年增长率？

查看试题解析
24. 如图所示，某小区要用篱笆围成一矩形花坛，花坛的一边用足够长的墙，另外三边所用的篱笆之和恰好为 $16$ 米．

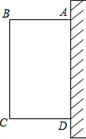(1)、求矩形 $A B C D$ 的面积（用 $s$ 表示，单位：平方米）与边 $A B$ （用 $x$ 表示，单位：米）之间的函数关系式（不要求写出自变量 $x$ 的取值范围）；怎样围，可使花坛面积最大？

(2)、如何围，可使此矩形花坛面积是 $30$ 平方米？

查看试题解析
25. 如图1、图2，在圆O中，OA=1，AB= $\sqrt{3}$ ，将弦AB与弧AB所围成的弓形（包括边界的阴影部分）绕点B顺时针旋转α度（0≤α≤360），点A的对应点是A′.

(1)、点O到线段AB的距离是；∠AOB=°；点O落在阴影部分（包括边界）时，α的取值范围是；

(2)、如图3，线段BD与优弧ACB的交点是D，当∠A′BA=90°时，说明点D在AO的延长线上；

(3)、当直线A′B与圆O相切时，求α的值并求此时点A′运动路径的长度.

查看试题解析

班级	平均分	中位数	众数	方差
八（1）	85	b	c	22.8
八（2）	a	85	85	19.2

金额/元	5	10	20	50	100
人数	4	16	15	9	6