江苏省镇江市2018-2019学年八年级上学期数学12月月考试卷

试卷更新日期：2019-09-30 类型：月考试卷

进入出卷网下载

一、单选题

1. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 点P（-4，5）关于y轴对称的点的坐标为（）

A、（4，－5） B、（－4，－5） C、（4，5） D、（5，4）

查看试题解析
3. 满足下列条件的△ABC不是直角三角形的是（）

A、BC=1，AC=2，AB= $\sqrt{3}$ B、BC：AC：AB=3：4：5 C、∠A+∠B=∠C D、∠A：∠B：∠C=3：4：5

查看试题解析
4. 在-0.1， $\sqrt{7}$ ， $\frac{1}{4}$ ， $- \frac{π}{2}$ ， $\sqrt[3]{8}$ ，0中，无理数的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 在同一平面直角坐标中，关于下列函数：①y =x＋1；②y =2x＋1；③y =2x－1；④y =－2x＋1的图像，说法不正确的是（）.

A、②和③的图像相互平行 B、②的图像可由③的图像平移得到 C、①和④的图像关于y轴对称 D、③和④的图像关于x轴对称

查看试题解析
6.
如图，∠BAC=110°，若MP和NQ分别垂直平分AB和AC，则∠PAQ的度数是（　　）

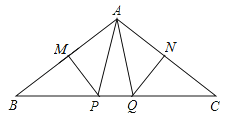A、20° B、40° C、50° D、60°

查看试题解析
7. 如图所示，已知△ABC中，AB=6，AC=9，AD⊥BC于D，M为AD上任一点，则MC²-MB²等于（）

A、9 B、35 C、45 D、无法计算

查看试题解析
8. 八个边长为1的正方形如图摆放在平面直角坐标系中，经过原点的一条直线l将这八个正方形分成面积相等的两部分，则该直线l的解析式为（）

A、y＝-x B、y＝- $\frac{3}{4}$ x C、y＝- $\frac{3}{5}$ x D、y＝- $\frac{9}{10}$ x

查看试题解析

二、填空题

9. 25的平方根是；64的立方根是．

查看试题解析
10. 比较大小：0.14 $π - 3$ .（填“＞”、“＝”或“＜”）

查看试题解析
11. 点A（－4 , 8）到x轴的距离是.

查看试题解析
12. 一次函数y=（m+2）x+1，若y随x的增大而增大，则m的取值范围是．

查看试题解析
13. 数2.185 $\times 10^{6}$ 精确到位.

查看试题解析
14. 直线 $y = 3 x - 6$ 与坐标轴所围成的三角形的面积是.

查看试题解析
15. 将点P向左平移2个单位长度，再向下平移1个单位长度得到P'（－1，3），则点P的坐标是.

查看试题解析
16. 如图，△ABC中，AB=AC=13，BC=10，D为BC中点，DE⊥AB于E，则DE=.

查看试题解析
17. 一次函数 $y = - 2 x + b$ 中，当 $x = 1$ 时， $y$ ＜1；当 $x = - 1$ 时， $y$ ＞0则 $b$ 的取值范围是.

查看试题解析
18. 无论a取什么实数，点A（2a ，6a+1）都在直线l上，则直线l的表达式是.

查看试题解析
19. 如图，点E在正方形ABCD内，满足∠AEB=90°，AE=3，BE=4，则阴影部分的面积是.

查看试题解析
20. 如图，在一张长为5cm，宽为4cm的长方形纸片上，现要剪下一个腰长为3cm的等腰三角形（要求：等腰三角形的一个顶点与长方形的一个顶点重合，其余的两个顶点在长方形的边上），则剪下的等腰三角形的底边的长为cm.

查看试题解析

三、解答题

21. 计算、解方程

(1)、 $\sqrt{25} - \sqrt[3]{- \frac{1}{8}} + \sqrt{\frac{9}{4}}$

(2)、(x＋3)²-36=0

(3)、8(x－1)³+27=0.

(4)、 ${(- 2)}^{2} - \sqrt[3]{64} - {(- 3)}^{0} + {(\frac{1}{3})}^{- 2}$

查看试题解析
22. 如图，点C，E，F，B在同一直线上，点A，D在BC异侧，AB∥CD，AE=DF，∠A=∠D.

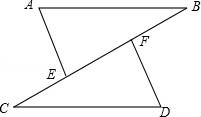(1)、求证：AB=CD；

(2)、若AB=CF，∠B=30°，求∠D的度数.

查看试题解析
23. 已知一次函数y＝kx＋b的图像经过点(－2，4)，且与正比例函数y＝2x的图像平行.

(1)、求一次函数y＝kx＋b的解析式；

(2)、求一次函数y＝kx＋b的图像与坐标轴所围成的三角形的面积；

(3)、若A(a，y₁)，B(a＋b，y₂)为一次函数y＝kx＋b的图像上两个点，试比较y₁与y₂的大小.

查看试题解析
24. 如图，将长方形ABCD沿着对角线BD折叠，使点C落在C′处，BC′交AD于点E.

(1)、试判断△BDE的形状，并说明理由；

(2)、若AB＝4，AD＝8，求△BDE的面积.

查看试题解析
25. 在△ABC中， AB、BC、AC三边的长分别为 $\sqrt{5}$ ， $\sqrt{10}$ ， $\sqrt{13}$ ，求这个三角形的面积.小明同学在解答这道题时，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图1所示.这样不需求△ABC的高，而借用网格就能计算出它的面积.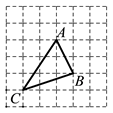

图1 图2 备用图

(1)、△ABC的面积为.

(2)、若△DEF的三边DE、EF、DF长分别为 $\sqrt{8}$ ， $\sqrt{13}$ ， $\sqrt{17}$ ，请在图2的正方形网格中画出相应的△DEF，并求出△DEF的面积为.

(3)、在△ABC中， AB=2 $\sqrt{5}$ ，AC=4，BC=2，以AB为边向△ABC外作△ABD（D与C在AB异侧），使△ABD为等腰直角三角形，则线段CD的长为.

查看试题解析
26. 如图，△ABC三个顶点的坐标分别为A（1，1）、B（4，2）、C（3，4）．

①画出△ABC关于y轴的对称图形△A₁B₁C₁ ，并写出B₁点的坐标；
②画出△ABC绕原点O旋转180°后得到的图形△A₂B₂C₂ ，并写出B₂点的坐标；
③在x轴上求作一点P，使△PAB的周长最小，并直接写出点P的坐标．

查看试题解析
27. 如图，已知函数y= $\frac{4}{3}$ x + 4的图象与坐标轴的交点分别为点A、B，点C与点B关于x轴对称，动点P、Q分别在线段BC、AB上（点P不与点B、C重合）.且∠APQ=∠ABO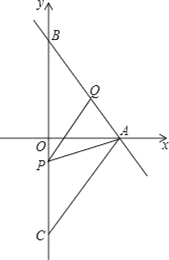

(1)、点A的坐标为， AC的长为；

(2)、判断∠BPQ与∠CAP的大小关系，并说明理由；

(3)、当△APQ为等腰三角形时，求点P的坐标.

查看试题解析