江苏省扬州市江都区邵樊片2018-2019学年八年级上学期数学第二次月考试卷

试卷更新日期：2019-09-30 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列图形是几家电信公司的标志，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在平面直角坐标系中，点P(-2，5)位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 下列各曲线中，不能表示y是x的函数的是（）

A、 B、 C、 D、

查看试题解析
4. 在（﹣ $\sqrt{2}$ ）⁰ ， $\sqrt[3]{8}$ ，0， $\sqrt{9}$ ， $\sqrt[3]{4}$ ，0.010010001…， $\frac{π}{2}$ ，﹣0.333…， $\sqrt{5}$ 中，无理数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
5. 估计 $\sqrt{13}$ ﹣1的值在（）

A、0到1之间 B、1到2之间 C、2到3之间 D、3至4之间

查看试题解析
6. 已知等腰三角形的一个外角等于110º，则该三角形的一个底角是（）

A、35º B、70º或110º C、70º D、55º或70º

查看试题解析
7. 某电视台“走基层”栏目的一位记者乘汽车赴320km外的农村采访，全程的前一部分为高速公路，后一部分为乡村公路．若汽车在高速公路和乡村公路上分别以某一速度匀速行驶，汽车行驶的路程y（单位：km）与时间x（单位：h）之间的关系如图所示，则下列结论正确的是（）

A、汽车在高速公路上的行驶速度为100km/h B、乡村公路总长为90km C、汽车在乡村公路上的行驶速度为60km/h D、该记者在出发后5h到达采访地

查看试题解析
8. 如图，Rt△ABC中，∠ACB＝90°， $A C = 3$ ， $B C = 4$ ，将边 $A C$ 沿 $C E$ 翻折，使点 $A$ 落在 $A B$ 上的点 $D$ 处；再将边 $B C$ 沿 $C F$ 翻折，使点 $B$ 落在 $C D$ 的延长线上的点 $B'$ 处，两条折痕与斜边 $A B$ 分别交于点 $E$ 、 $F$ ，则线段 $B' F$ 的长为（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{2}{3}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析

二、填空题

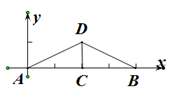
9. 把直线y=2x向右平移5个单位得到直线l，则直线l的解析式为.

查看试题解析
10. 用四舍五入法对31500取近似数，并精确到千位，用科学记数法可表示为.

查看试题解析
11. 函数y= $\sqrt{1 - 2 x}$ 的自变量x的取值范围为.

查看试题解析
12. 若函数 $y = (m + 1) x^{m^{2}} + 3$ 是y关于x的一次函数，则m=.

查看试题解析
13. 我们定义：如果点P（x，y）的横坐标x、纵坐标y都是整数，且满足x+y=xy，那么点P叫做“酷点”，根据定义，写一个“酷点”的坐标.

查看试题解析
14. 如图，长为8 cm的橡皮筋放置在x轴上，固定两端A和B，然后把中点C向上拉升3 cm到点D，则橡皮筋被拉长了 cm.

查看试题解析
15. 若a₁=1，a₂= $\sqrt{2}$ ，a₃= $\sqrt{3}$ ，a₄=2，…，按此规律在a₁到a₂₀₁₈中，共有无理数个.

查看试题解析
16. 如图，四边形ABCD中，AC、BD是对角线，△ABC是等边三角形，∠ADC＝30°，AD＝3，BD＝5，则CD的长为.

查看试题解析
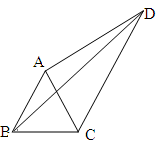17. 如图，在ΔABC与ΔDEF中，如果AB=DE，BE=CF，只要加上条件(写一个就可以)，就可证明ΔABC≌ΔDEF；并用你所选择的条件加以证明。

查看试题解析

三、解答题

18. 计算及解方程

(1)、解方程：(x－1)³=27

(2)、计算： $\sqrt{25} - \sqrt[3]{- 27} + \sqrt{\frac{1}{4}}$

查看试题解析
19. 如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A(-3，5)，B(-2，1)，C(-1，3).

(1)、①画出△ABC关于x轴的对称图形△A₁B₁C₁；
②画出△A₁B₁C₁沿x轴向右平移4个单位长度后得到的△A₂B₂C₂；

(2)、如果AC上有一点M(a，b)经过上述两次变换，那么对应A₂C₂上的点M₂的坐标是.

查看试题解析
20. 求一个正数的算术平方根，有些数可以直接求得，如 $\sqrt{4}$ ，有些数则不能直接求得，如 $\sqrt{5}$ ，但可以通过计算器求. 还有一种方法可以通过一组数的内在联系，运用规律求得，请同学们观察下表：

n

16

0.16

0.0016

1600

160000

…

$\sqrt{n}$

4

0.4

0.04

40

400

…

(1)、若 $\frac{a}{b} = 100$ ，则 $\frac{\sqrt{a}}{\sqrt{b}} =$

(2)、根据你发现的规律，探究下列问题：已知 $\sqrt{2.06}$ ≈1.435，则：
① $\sqrt{0.0206}$ ≈；

② $\sqrt{20600}$ ≈；

(3)、根据上述探究过程类比研究一个数的立方根已知 $\sqrt[3]{2}$ ≈1.260，则 $\sqrt[3]{2000}$ ≈ .

查看试题解析
21. 已知y+3与x+2成正比例，且当x=3时，y=7；

(1)、求出y与x之间的函数关系式；

(2)、当x=﹣1时，求y的值；

(3)、当y=0时，求x的值．

查看试题解析
22. 如图所示，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F．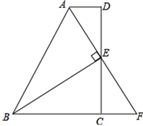

求证：

(1)、FC=AD；

(2)、AB=BC+AD．

查看试题解析
23. 如图，已知一次函数 $y = - x + 2$ 的图像与 $y$ 轴交于点 $A$ ，一次函数 $y = k x + b$ 的图像过点 $B (0 ， 4)$ ，且与 $x$ 轴及 $y = - x + 2$ 的图像分别交于点 $C$ 、 $D$ ， $D$ 点坐标为 $(- \frac{2}{3} ， n)$ .

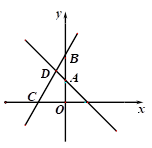(1)、求n的值及一次函数 $y = k x + b$ 的解析式.

(2)、求四边形 $A O C D$ 的面积.

查看试题解析
24. 如图， $C$ 为线段 $B D$ 上一动点，分别过点 $B ， D$ 作 $A B ⊥ B D$ ， $E D ⊥ B D$ ，连接 $A C ， E C$ .已知 $A B = 5 ， D E = 1 ， B D = 8$ ，设 $C D = x$ .

(1)、用含 $x$ 的代数式表示 $A C + C E$ 的值；

(2)、探究：当点 $C$ 满足什么条件时， $A C + C E$ 的值最小?最小值是多少?

(3)、根据(2)中的结论，请构造图形求代数式 $\sqrt{x^{2} + 4} + \sqrt{{(12 - x)}^{2} + 9}$ 的最小值.

查看试题解析
25. 若两个一次函数y=k₁x+b₁（k₁≠0），y=k₂x+b₂（k₂≠0），则称函数y=（k₁+k₂）x+b₁b₂为这两个函数的组合函数.

(1)、一次函数y=3x+2与y=﹣4x+3的组合函数为；若一次函数y=ax﹣2，y=﹣x+b的组合函数为y=3x+2，则a= ， b=.

(2)、已知一次函数y=﹣x+b与y=kx﹣3的组合函数的图象经过第一、二、四象限，求常数k、b满足的条件；

(3)、已知一次函数y=﹣2x+m与y=3mx﹣6，则不论何值，它们的组合函数一定经过的定点坐标是.

查看试题解析
26. 如图，在平面直角坐标系中，O为坐标原点，正方形OABC的面积为16，点D的坐标为（0，3）.将直线BD沿y轴向下平移d个单位得到直线l（0＜d≤4）.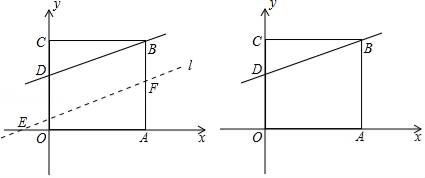

(1)、则点B的坐标为；

(2)、当d=1时，求直线l的函数表达式；

(3)、设直线l与x轴相交于点E，与边AB相交于点F，若CE=CF，求d的值并直接写出此时∠ECF的度数.

查看试题解析

n	16	0.16	0.0016	1600	160000	…
$\sqrt{n}$	4	0.4	0.04	40	400	…