江苏省海安县2018-2019学年八年级上学期数学第一次月考试卷
试卷更新日期：2019-09-30 类型：月考试卷
一、单选题
-
1. 点P(3，－4)关于y轴对称的点的坐标为（ ）A、(－3， 4) B、(3，4) C、(－3，－4) D、(3，－4)2. 在△ABC中，∠A=70°，∠B=60°，∠ACD是△ABC的一个外角，∠ACD的度数为（ ）A、50° B、60° C、70° D、130°3. 下列各组数中，能作为一个三角形三边边长的是（ ）
A、1，1，2 B、1，2，4 C、2，3，4 D、2，3，54. 如图，在△ABC中有四条线段DE，BE，EF，FG，其中有一条线段是△ABC的中线，则该线段是（ ）
A、线段DE B、线段BE C、线段EF D、线段FG5. 如图所示，图中x的值是（ ）
A、50 B、60 C、70 D、806. 如图，BE、CF都是△ABC的角平分线，且∠BDC=110°，则∠A=（ ）
A、50° B、40° C、70° D、35°7. 如图，已知BD是△ABC的角平分线，ED是BC的垂直平分线，∠BAC=90°，CE=4，△ABD的周长为12，则△ABC的周长为（ ）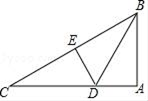
A、12 B、16 C、20 D、248. 如图，△ABC中，AD是BC边上的高，AE、BF分别是∠BAC、∠ABC的平分线，∠BAC=50°，∠ABC=60°，则∠EAD+∠ACD=（ ）
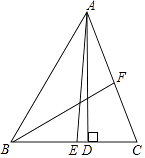A、75° B、80° C、85° D、90°9. 如图，将一张三角形纸片ABC的一角折叠，使点A落在△ABC外的A'处，折痕为DE．如果∠A=α，∠CEA′=β，∠BDA'=γ，那么下列式子中正确的是（ ）
A、γ=2α+β B、γ=α+2β C、γ=α+β D、γ=180°﹣α﹣β10. 如图，四边形ABCD中，AB=AD，AC=5，∠DAB=∠DCB=90°，则四边形ABCD的面积为（ ）
A、15 B、12.5 C、14.5 D、17二、填空题
-
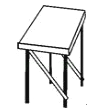
11.
如图，李叔叔家的凳子坏了，于是他给凳子加了两根木条，这样凳子就比较牢固了，他所应用的数学原理是 ．
12. 如图，线段AC与BD交于点O，且OA=OC， 请添加一个条件，使△OAB≌△OCD，这个条件是 .
13. 在平面直角坐标系中，点 A的坐标是(-1,2) .作点A关于x 轴的对称点，得到点A1 ，再将点A1 向下平移 4个单位，得到点A2 ，则点A2 的坐标是.14. 如果两个三角形的两条边和其中一边上的高对应相等，那么这两个三角形的第三边所对的角的关系是.15. 当三角形中一个内角α是另一个内角β的一半时，我们称此三角形为“半角三角形”，其中α称为“半角”．如果一个“半角三角形”的“半角”为20°，那么这个“半角三角形”的最大内角的度数为 ．三、解答题
-
16. 如图，已知点M、N和∠AOB，求作一点P，使P到∠AOB两点的距离相等，且到点M、N的距离相等.
17. 一个多边形的内角和比它外角和的3少180°，求这个多边形的边数.18. 如图，在△ABC中，∠BAC=40°，∠B=75°，AD是△ABC的角平分线，求∠ADC的度数.
19. 如图.在△ABC中，AD是角平分线，且BD=CD，DE⊥AB，DF⊥AC，垂足分别为E、F.求证：EB=FC.
20. 如图所示，△ADF和△BCE中，∠A＝∠B，点D，E，F，C在同一条直线上，有如下三个关系式：①AD＝BC；②DE＝CF；③BE∥AF；
(1)、请你用其中两个关系式作为条件，另一个作为结论，写出所有你认为正确的命题；（用序号写出命题的书写形式，如：如果 ，那么 ）(2)、选择（1）中你写的一个命题，说明它的正确性21. 如图所示，已知AE⊥AB，AF⊥AC，AE=AB，AF=AC.试判断线段EC与BF的关系并证明.
22. 数学兴趣小组在活动时，老师提出了这样一个问题：如图1，在△ABC中，AB=8，AC=6，D是BC的中点，求BC边上的中线AD的取值范围.小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使DE=AD，再证明“△ADC≌△EDB”.
(1)、探究得出AD的取值范围是；(2)、（问题解决）如图2，△ABC中，∠B=90°，AB=2，AD是△ABC的中线，CE⊥BC，CE=4，且∠ADE=90°，求AE的长.23. 已知点P为∠EAF平分线上一点，PB⊥AE于B，PC⊥AF于C，点M，N分别是射线AE，AF上的点，且PM=PN.
(1)、如图1，当点M在线段AB上，点N在线段AC的延长线上时，求证：BM=CN；(2)、在（1）的条件下，直接写出线段AM，AN与AC之间的数量关系 ；(3)、如图2，当点M在线段AB的延长线上，点N在线段AC上时，若AC：PC=2：1，且PC=4，求四边形ANPM的面积.