江苏省东台市第五联盟2018-2019学年八年级上学期数学12月月考试卷
试卷更新日期:2019-09-30 类型:月考试卷
一、单选题
-
1. 如图,小手盖住的点的坐标可能为( )
 A、(3,-4) B、(-4,3) C、(-4,-3) D、(3,4)2. 如图,△ABC中,AB=AC,D是BC中点,下列结论中不正确的是( )
A、(3,-4) B、(-4,3) C、(-4,-3) D、(3,4)2. 如图,△ABC中,AB=AC,D是BC中点,下列结论中不正确的是( )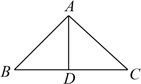 A、 B、AD⊥BC C、AD平分∠BAC D、BC=2AD3. 一个等腰三角形两边的长分别为2和5,那么这个三角形的周长是( )A、9 B、12 C、9或12 D、154. 下列线段长中,能构成直角三角形的是( )A、1.5,2,3 B、2,3,4 C、 , , D、8,15,175. 在 , , , , 中,无理数的个数是( )A、 个 B、 个 C、 个 D、 个6. 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A、 B、AD⊥BC C、AD平分∠BAC D、BC=2AD3. 一个等腰三角形两边的长分别为2和5,那么这个三角形的周长是( )A、9 B、12 C、9或12 D、154. 下列线段长中,能构成直角三角形的是( )A、1.5,2,3 B、2,3,4 C、 , , D、8,15,175. 在 , , , , 中,无理数的个数是( )A、 个 B、 个 C、 个 D、 个6. 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )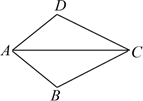 A、 B、 C、 D、7. 估计 的值在( )A、 到 之间 B、 到5之间 C、 到 之间 D、 到 之间8. 小刚从家去学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车匀速行驶一段时后到达学校,小刚从家到学校行驶路程s(单位:m)与时间r(单位:min)之间函数关系的大致图象是( )A、
A、 B、 C、 D、7. 估计 的值在( )A、 到 之间 B、 到5之间 C、 到 之间 D、 到 之间8. 小刚从家去学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车匀速行驶一段时后到达学校,小刚从家到学校行驶路程s(单位:m)与时间r(单位:min)之间函数关系的大致图象是( )A、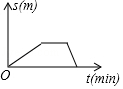 B、
B、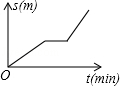 C、
C、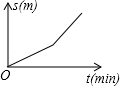 D、
D、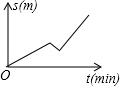
二、填空题
-
9. 在平面直角坐标系中点 ,关于 轴对称的点的坐标为(-2,-4),则点 的坐标是.10. 被誉为“中国天眼”的世界上最大的单口径球面射电望远镜FAST的反射面总面积为249900m2 , 请将249900精确到万位,并用科学记数法表示为.11. 已知函数 ,当 时, 是 的正比例函数.12. 如图,在中国象棋的残局上建立平面直角坐标系,如果“相”和“兵”的坐标分别是(3,﹣1)和(﹣3,1),那么“卒”的坐标为.
 13. 如图,正方形 的边 落在数轴上,点 表示的数为 ,点 表示的数为 ,以 点为圆心, 长为半径作圆弧与数轴交于点 ,则点 表示的数为.
13. 如图,正方形 的边 落在数轴上,点 表示的数为 ,点 表示的数为 ,以 点为圆心, 长为半径作圆弧与数轴交于点 ,则点 表示的数为.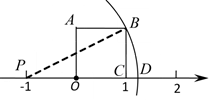 14. 如图,在△ABC 中,AB、AC 的垂直平分线分别交 BC 于点 E、F.若BC=10cm,则△AEF 的周长为cm.
14. 如图,在△ABC 中,AB、AC 的垂直平分线分别交 BC 于点 E、F.若BC=10cm,则△AEF 的周长为cm.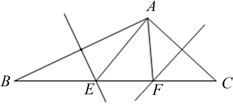 15. 小红帮弟弟荡秋千(图1),秋千离地面的高度 与摆动时间 之间的关系如图2所示,则秋千摆动第一个来回需s.
15. 小红帮弟弟荡秋千(图1),秋千离地面的高度 与摆动时间 之间的关系如图2所示,则秋千摆动第一个来回需s. 16. 如图,等边三角形 的边长为 , 是 边上的高 所在的直线,点 为直线 上的一动点,连接 并将 绕点 逆时针旋转 至 ,连接 ,则 的最小值为.
16. 如图,等边三角形 的边长为 , 是 边上的高 所在的直线,点 为直线 上的一动点,连接 并将 绕点 逆时针旋转 至 ,连接 ,则 的最小值为.
三、解答题
-
17.(1)、计算:(2)、解方程:18. 已知如图,四边形 中, , ,求证: .
 19. 已知:如图,在 中过点 、 分别作 , ,垂足分别为 、 ,且 .求证: .
19. 已知:如图,在 中过点 、 分别作 , ,垂足分别为 、 ,且 .求证: . 20. 如图,将边长为a与b、对角线长为c的长方形纸片 ,绕点 顺时针旋转 得到长方形 ,连接 ,则四边形 为梯形,请通过该图验证勾股定理(求证: ).
20. 如图,将边长为a与b、对角线长为c的长方形纸片 ,绕点 顺时针旋转 得到长方形 ,连接 ,则四边形 为梯形,请通过该图验证勾股定理(求证: ). 21. “绿色出行,低碳健身”已成为广大市民的共识.为方便市民出行,东台市推出了公共自行车系统,收费以小时为单位,每次使用不超过1小时的免费,超过1小时后,不足1小时的部分按1小时收费.小红同学通过调查得知,自行车使用时间为3小时,收费2元;使用时间为4小时,收费3元.她发现当使用时间超过1小时后用车费用与使用时间之间存在一次函数的关系.(1)、设使用自行车的费用为 元,使用时间为 小时( 为大于1的整数),求 与 的函数解析式;(2)、若小红此次使用公共自行车5小时,则她应付多少元费用?(3)、若小红此次使用公共自行车付费6元,求她所使用自行车的时间.22. 已知:如图, ,M、N分别是AC、BD的中点.
21. “绿色出行,低碳健身”已成为广大市民的共识.为方便市民出行,东台市推出了公共自行车系统,收费以小时为单位,每次使用不超过1小时的免费,超过1小时后,不足1小时的部分按1小时收费.小红同学通过调查得知,自行车使用时间为3小时,收费2元;使用时间为4小时,收费3元.她发现当使用时间超过1小时后用车费用与使用时间之间存在一次函数的关系.(1)、设使用自行车的费用为 元,使用时间为 小时( 为大于1的整数),求 与 的函数解析式;(2)、若小红此次使用公共自行车5小时,则她应付多少元费用?(3)、若小红此次使用公共自行车付费6元,求她所使用自行车的时间.22. 已知:如图, ,M、N分别是AC、BD的中点. (1)、求证:MN⊥BD;;(2)、若AC=10,BD=8,求MN.
(1)、求证:MN⊥BD;;(2)、若AC=10,BD=8,求MN.

