江苏省东台市第四联盟2018-2019学年八年级上学期数学12月月考试卷
试卷更新日期：2019-09-30 类型：月考试卷
一、单选题
-
1. 下列四个实数中是无理数是（ ）A、0 B、π C、 D、2. 下列说法正确的是（ ）A、两个等边三角形一定全等 B、面积相等的两个三角形全等 C、形状相同的两个三角形全等 D、全等三角形的面积一定相等3. 若a＞0，b＜－2，则点（a，b＋2）在（ ）A、第四象限 B、第三象限 C、第二象限 D、第一象限4. 在△ABC中，AB＝AC，BD为△ABC的高，如果∠BAC＝40°，则∠CBD的度数是（ ）
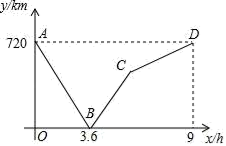
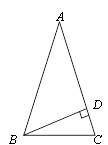A、70° B、40° C、20° D、30°5. 已知汽车油箱内有油40L，每行驶100km耗油10L，则汽车行驶过程中油箱内剩余的油量Q （L）与行驶路程s（km）之间的函数表达式是（ ）A、Q＝40＋ B、Q＝40﹣ C、Q＝40﹣ D、Q＝40＋6. 将直线y=-2x向下平移两个单位，所得到的直线为（ ）A、y=-2（x+2） B、y=-2（x-2） C、y=-2x-2 D、y=-2x+27. 下列条件中，不能判断△ABC为直角三角形的是（ ）A、a=1.5 b=2 c=2.5 B、a：b：c=5：12：13 C、∠A＋∠B=∠C D、∠A：∠B：∠C=3：4：58. 某水果超市以每千克3元的价格购进某种水果若干千克，销售一部分后，根据市场行情降价销售，销售额y（元）与销售量x（千克）之间的关系如图所示．若该水果超市销售此种水果的利润为110元，则销售量为（ ）
A、130千克 B、120千克 C、100千克 D、80千克二、填空题
-
9. 9的算术平方根是 ， = ， ﹣ = ．10. 比较大小： －30.（填“﹥”、“﹦”或“﹤”号）11. 在平面直角坐标系中，点P（-4，3）关于 y 轴的对称点坐标为.12. 2017年我市参加中考的学生人数大约为2.60×104人，对于这个用科学记数法表示的近似数，它精确到了位.13. 若 有意义，则x 的取值范围是.14. 若正比例函数的图象过点A(3，－6)，则该正比例函数的表达式为.15. 如果点B (n2－4，－n－3) 在y轴上，那么n=16. 如图，直线l1：y=x+n–2与直线l2：y=mx+n相交于点P(1，2).则不等式mx+n<x+n–2的解集为.
17. 如图，在数轴上，点A、B表示的数分别为0、2，BC⊥AB于点B，且BC=1，连接AC，在AC上截取CD=BC，以A为圆心，AD的长为半径画弧，交线段AB于点E，则点E表示的实数是.
18. 如图，在平面直角坐标系中，△P1OA1 ， △P2A1A2 ， △P3A2A3 ， …都是等腰直角三角形，其直角顶点P1(3，3)，P2 ， P3 ， …均在直线y＝﹣ x+4上.设△P1OA1 ， △P2A1A2 ， △P3A2A3 ， …的面积分别为S1 ， S2 ， S3 ， …，依据图形所反映的规律，S2018=.
三、解答题
-
19. 求下列各式中的x：(1)、（x＋2）2＝4；(2)、1＋（x﹣1）3＝－7.20. 操作探究：如图，△ABC在平面直角坐标系中，其中，点A，B，C的坐标分别为A（–2，1），B（–4，5），C（–5，2）.
(1)、作△ABC关于直线l：x=–1对称的△A1B1C1 ， 其中，点A， B，C的对称点分别为点A1 ， B1 ， C1；(2)、写出点C1的坐标；(3)、在平面直角坐标系中有一点P位于第四象限，其坐标表示为P（m，n），则点P关于直线l的对称点Q的坐标表示为.21. 如图，△ABC中，BA＝BC，点D是AB延长线上一点，DF⊥AC于F交BC于E.求证：△DBE是等腰三角形.
22. 如图，直线l1：y=x+1与直线l2：y=mx+n相交于点P（1，b）.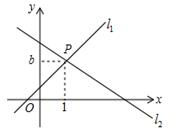
(1)、求b的值；(2)、解关于x、y的方程组 ，请你直接写出它的解；(3)、直线l3：y=nx+m是否也经过点P？请说明理由.23. 如图，在平面直角坐标系中，点A、B的坐标分别为（2，3）和（0，2）.
(1)、AB的长为；(2)、点C在y轴上，△ABC是等腰三角形，写出所有满足条件的点C的坐标.24. 某年级380名师生秋游，计划租用7辆客车，现有甲、乙两种型号客车，它们的载客量和租金如表．甲种客车
乙种客车
载客量（座/辆）
60
45
租金（元/辆）
550
450
(1)、设租用甲种客车x辆，租车总费用为y元．求出y（元）与x（辆）之间的函数表达式；(2)、当甲种客车有多少辆时，能保障所有的师生能参加秋游且租车费用最少，最少费用是多少元？
