湖北省武汉六初、六中上智2018-2019学年八年级上学期数学12月月考试卷

试卷更新日期：2019-09-30 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列计算中正确的是（）

A、a²＋a³＝2a⁵ B、a⁴÷a＝a⁴ C、a²·a⁴＝a⁸ D、(－a²)³＝－a⁶

查看试题解析
2. 下列各式中能用平方差公式的是（）

A、(x＋y)(y＋x) B、（x＋y)(y－x) C、(x＋y)(－y－x) D、(－x＋y)(y－x)

查看试题解析
3. 下列计算正确的是（）

A、－2(x²y³)²＝－4x⁴y⁶ B、8x³－3x²－x³＝4x³ C、a²b(－2ab²)＝－2a³b³ D、－(x－y)²＝－x²－2xy－y²

查看试题解析
4. 下列因式分解正确的是（）

A、4a²－4a＋1＝4a(a－1)＋1 B、x²－4y²＝(x＋4y)(x－4y) C、 $\frac{9}{4}$ x²－x＋ $\frac{1}{9}$ ＝ ${(\frac{3}{2} x - \frac{1}{3})}^{2}$ D、2xy－x²－y²＝－(x＋y)²

查看试题解析
5. 已知二次三项式2x²＋bx＋c因式分解的结果为2(x－3)(x＋1)，则b，c的值为（）

A、b＝3，c＝－1 B、b＝－6，c＝2 C、b＝－6，c＝4 D、b＝－4，c＝－6

查看试题解析
6. 多项式m²－4n²与m²－4mn＋4n²的公因式是（）

A、（m＋2n）（m－2n) B、m＋2n C、m－2n D、（m＋2n）（m－2n）²

查看试题解析
7. 平面内点 A(－1，2)和点 B(－1，－2)的对称轴是（）

A、x 轴 B、y 轴 C、直线 y＝4 D、直线 x＝－1

查看试题解析
8. 若分式 $\frac{x^{2} - 4}{2 x - 4}$ 的值为零，则x等于（）

A、2 B、﹣2 C、±2 D、0

查看试题解析
9. 如果9x²+kx+25是一个完全平方式，那么k的值是（）

A、30 B、±30 C、15 D、±15

查看试题解析
10. 如图，已知∠MON＝30°，点 A₁、A₂、A₃、…在射线 ON 上，点 B₁、B₂、B₃、…在射线 OM 上；△A₁B₁A₂、△A₂B₂A₃、△A₃B₃A₄、…均为等边三角形.若 OA₁＝1，则△A₂₀₁₅B₂₀₁₅A₂₀₁₆ 的边长为（）

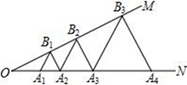A、4028 B、4030 C、2²⁰¹⁴ D、2²⁰¹⁵

查看试题解析

二、填空题

11. 计算：a $^{2}$ ·(－2a $^{2}$ ) $^{3}$ ＝, ${(- \frac{1}{2})}^{2018} \cdot {(- 2)}^{2019} =$ .

查看试题解析
12. 若分式 $\frac{x + 1}{x - 1}$ 有意义，x 的取值范围是.

查看试题解析
13. 已知(a＋b)²＝7，(a－b)²＝4，则 ab 的值为.

查看试题解析
14. 如图为杨辉三角表，它可以帮助我们按规律写出(a＋b)ⁿ（其中 n 为正整数）展开式的系数，请仔细观察表中规律，写出(a＋b)⁵的展开式.

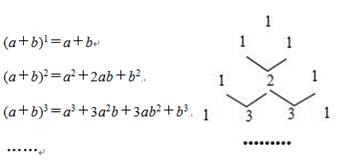
(a＋b)⁵＝

查看试题解析
15. 如图，四边形 ABCD 中，AB⊥AD，BC⊥DC，点 M、N 分别是 AB、BC 边上的动点，∠B＝56°.当△DMN 的周长最小时，则∠MDN 的度数是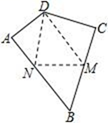

查看试题解析

三、解答题

16. 直角三角形纸片 ABC 中，∠ACB＝90°，AC≤BC.如图，将纸片沿某条直线折叠，使点 A 落在直角边 BC 上，记落点为 D.设折痕与 AB、AC 边分别交于点 E、点 F，当折叠后的△CDF 与△BDE 均为等腰三角形，那么纸片中∠B 的度数是

查看试题解析
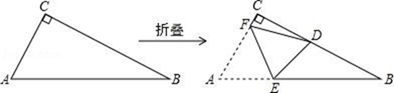17. 计算：

(1)、(2m＋n)²－(m＋n)(m－n)－n²

(2)、 $\frac{a^{2} - b^{2}}{a^{2} + 2 a b + b^{2}} \cdot \frac{a + b}{a - 2 b}$

查看试题解析
18. 因式分解：

(1)、2a²－18

(2)、－2x²y＋8xy－8y

查看试题解析
19. 先化简，再求值：

(1)、[(x－y)²＋(x＋y)(x－y)]÷2x，其中 x＝3，y＝－2

(2)、已知 $\frac{3 a + 1}{a} = 0$ ，求 $\frac{a^{2} - 2 a + 1}{a^{2} - 2 a} \div (a - 1) \cdot \frac{2 - a}{a - 1}$ 的值.

查看试题解析
20. 如图，△ABC 中，A(－2，3)、B(－3，1)、C(－1，2)

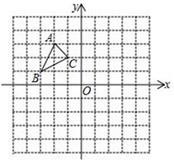(1)、作△ABC 关于直线 x＝1 对称的图形△A₁B₁C₁ ，写出三顶点 A₁、B₁、C₁的坐标

(2)、在 x 轴上求作一点 D，使四边形 ABDC 的周长最小（保留作图痕迹，不要求写作法和证明）

查看试题解析
21. 已知 x²＋2x＋y²－10y＋26＝0，求：

(1)、x＋2y 的平方根.

(2)、2y＋2x 的立方根.

查看试题解析
22. 如图，△ABC 是边长为 6 cm 的等边三角形，P 从点 A 岀发沿 AC 边向 C 运动，与此同时 Q 从 B 出发以相同的速度沿 CB 延长线方向运动.当 P 到达 C 点时，P、Q 停止运动，连接 PQ 交 AB 于 D

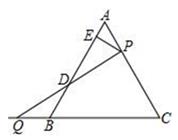(1)、设 P、Q 的运动速度为 1 cm/s，当运动时间为多少时，∠BQD＝30°？

(2)、过 P 作 PE⊥AB 于 E，在运动过程中线段 ED 的长是否发生变化？如果不变，求出线段 ED的长；如果变化请说明理由

查看试题解析
23. 若 a、b、c 为△ABC 的三边，且满足 a²＋b²＋c²＝ab＋ac＋bc.点 D 是 AC边的中点，以点 D 为顶点作∠FDE＝120°，角的两边分别与直线 AB 和 BC 相交于点 F 和点 E

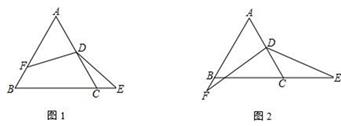(1)、试判断△ABC 的形状，说明理由

(2)、如图 1，将△ABC 图形中∠FDE＝120°绕顶点 D 旋转，当两边 DF、DE 分别与边 AB 和射线BC 相交于点 F、E 时，三线段 BE、BF、AB 之间存在什么关系？证明你的结论

(3)、如图 2，当角两边 DF、DE 分别与射线 AB 和射线 BC 相交两点 F、E 时，三线段 BE、BF、AB 之间存在什么关系

查看试题解析
24. 已知如图，在平面直角坐标系中，点 B(m，0)、A(n，0)分别是 x 轴轴上两点，且满足多项式(x²＋mx＋8)(x²－3x＋n)的积中不含 x³项和 x²项，点 P(0，h)是 y 轴正半轴上的动点

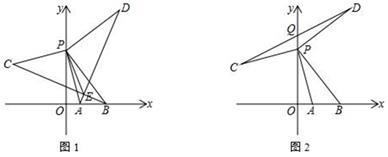(1)、求三角形△ABP 的面积（用含 h 的代数式表示）

(2)、过点 P 作 DP⊥PB，CP⊥PA，且 PD＝PB，PC＝AP
① 连接 AD、BC 相交于点 E，再连 PE，求∠BEP 的度数

② 连 CD 与 y 轴相交于点 Q，当动点 P 在 y 轴正半轴上运动时，线段 PQ 的长度变不变？如果不变，请求出其值；如果变化，请求出其变化范围

查看试题解析