浙江省杭州市十三中教育集团2019-2020学年九年级上学期数学开学试卷
试卷更新日期:2019-09-30 类型:开学考试
一、选择题(共10个小题,满分30分,每小题3分)
-
1. 下列地铁标志图形中,属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列函数中,y关于x的二次函数是( )A、y=ax2+bx+c B、y=x(x-1) C、y= D、y=(x-1)2-x23. 已知二次根式 ,则a的取值范围是( )A、a< B、a≤ C、a> D、a≥4. 若关于x的一元二次方程(k+2)x2-3x+1=0有实数根,则k的取值范围是( )A、k< 且k≠-2 B、k≤ C、k≤ 且k≠-2 D、k≥5. 若不等式k< <k+1成立,则整数k的值为( )A、6 B、7 C、8 D、96. 在反比例函数y= 图象上有三个点A(x1 , y1)、B(x2 , y2)、C(x3 , y3),若x1<0<x2<x3 , 则下列结论正确的是( )A、y1<y3<y2 B、y2<y3<y1 C、y3<y1<y2 D、y3<y2<y17. 如图,在▱ABCD中,AC与BD交于点O,点E,F是对角线AC上的两点,下列条件中不一定能判定四边形DEBF是平行四边形的是( )
2. 下列函数中,y关于x的二次函数是( )A、y=ax2+bx+c B、y=x(x-1) C、y= D、y=(x-1)2-x23. 已知二次根式 ,则a的取值范围是( )A、a< B、a≤ C、a> D、a≥4. 若关于x的一元二次方程(k+2)x2-3x+1=0有实数根,则k的取值范围是( )A、k< 且k≠-2 B、k≤ C、k≤ 且k≠-2 D、k≥5. 若不等式k< <k+1成立,则整数k的值为( )A、6 B、7 C、8 D、96. 在反比例函数y= 图象上有三个点A(x1 , y1)、B(x2 , y2)、C(x3 , y3),若x1<0<x2<x3 , 则下列结论正确的是( )A、y1<y3<y2 B、y2<y3<y1 C、y3<y1<y2 D、y3<y2<y17. 如图,在▱ABCD中,AC与BD交于点O,点E,F是对角线AC上的两点,下列条件中不一定能判定四边形DEBF是平行四边形的是( )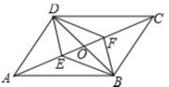 A、AE=CF B、DE=BF C、∠ADE=∠CBF D、∠AED=∠CFB8. 已知ab<0,一次函数y=ax-b与反比例函数y= 在同一坐标系中的图象可能是( )A、
A、AE=CF B、DE=BF C、∠ADE=∠CBF D、∠AED=∠CFB8. 已知ab<0,一次函数y=ax-b与反比例函数y= 在同一坐标系中的图象可能是( )A、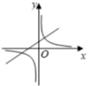 B、
B、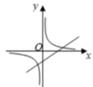 C、
C、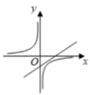 D、
D、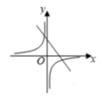 9. 如图,在菱形纸片ABCD中,对角线AC、BD长分别为16、12,折叠纸片使点A落在DB上,折痕交AC于点P,则DP的长为( )
9. 如图,在菱形纸片ABCD中,对角线AC、BD长分别为16、12,折叠纸片使点A落在DB上,折痕交AC于点P,则DP的长为( )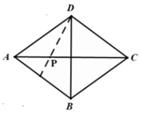 A、3 B、 C、3 D、310. 规定:如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根是另一个根的2倍,则称这样的方程为“倍根方程”现有下列结论:
A、3 B、 C、3 D、310. 规定:如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根是另一个根的2倍,则称这样的方程为“倍根方程”现有下列结论:①方程x2+2x-8=0是倍根方程;②若关于x的方程x2+ax+2=0是倍根方程,则a=±3;③若(x-3)(mx-n)=0是倍根方程,则n=6m或3n=2m;④若点(m,n)在反比例函数y= 的图象上,则关于x的方程mx2-3x+n=0是倍根方程。上述结论中正确的有( )
A、①② B、③④ C、②③ D、②④二、填空题(共6小题,满分24分,每小题4分)
-
11. 一个多边形的每个外角都等于72°,则这个多边形的边数为 .12. 已知一组数据5,8,10,x,9的众数是8,那么这组数据的方差是 。13. 若二次函数y=ax2-bx+5(a≠0)的图象与x轴交于(1,0),则b-a+2014的值是。14. 如图,在△ABC中,CD平分∠ACB,AD⊥CD,垂足为D,AD交BC于点F,E为AB的中点,连接DE,AC=15,BC=27;则DE=。
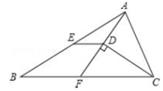 15. 如图,在平面直角坐标系中,点A在抛物线y=x2-2x+3上运动,过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为。
15. 如图,在平面直角坐标系中,点A在抛物线y=x2-2x+3上运动,过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为。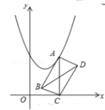 16. 如图,在正方形ABCD中,AB=6,E为CD上一动点,AE交BD于点F,过F作FH⊥AE,交BC于点H,连结AH、HE,AH与BD交于点G,下列结论:①AF=HE,②∠HAE=45°,③BG2+DF2=GF2 , ④△CEH的周长为12,其中正确的结论有。
16. 如图,在正方形ABCD中,AB=6,E为CD上一动点,AE交BD于点F,过F作FH⊥AE,交BC于点H,连结AH、HE,AH与BD交于点G,下列结论:①AF=HE,②∠HAE=45°,③BG2+DF2=GF2 , ④△CEH的周长为12,其中正确的结论有。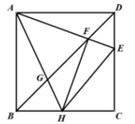
三、解答题(本题有8小题,共66分) 1
-
17. 随着移动互联网的快速发展,基于互联网的共享单车应运而生。为了解某单位使用共享单车的情况,该单位有200名员工,某研究小组随机采访10位员工,得到这10位员工一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9。
(1)、这组数据的中位数是 , 众数是;(2)、试用平均数估计该单位员工一周内使用共享单车的总次数.18. 在平面直角坐标系中,二次函数y=ax2+bx+3的图象经过点A(3,0)和点B(4,3)。
(1)、求二次函数的表达式;(2)、求二次函数图象的顶点坐标和对称轴.19. 已知关于x的一元二次方程x2-(m+2)x+2m=0。(1)、求证:不论m为何值,该方程总有两个实数根;(2)、若此方程的一个根是1,请求出方程的另一个根,并求出以此两根为边长的直角三角形的周长。20. 如图,在△ABC中,D、E分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连结CF。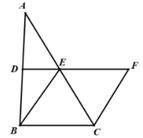 (1)、求证:四边形BCFE是菱形;(2)、若CE=5,∠BEF=120°,求菱形BCFE的面积。21. 直线y=3x与反比例函数y= 的图象交于A(1,m)和点B。
(1)、求证:四边形BCFE是菱形;(2)、若CE=5,∠BEF=120°,求菱形BCFE的面积。21. 直线y=3x与反比例函数y= 的图象交于A(1,m)和点B。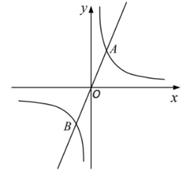 (1)、求m、k的值,并直接写出点B的坐标;(2)、过点P(t,0)(-1≤t≤1且t≠0)作x轴的垂线分别交直线y=3x与反比例函数y= 的图象于点E,F。
(1)、求m、k的值,并直接写出点B的坐标;(2)、过点P(t,0)(-1≤t≤1且t≠0)作x轴的垂线分别交直线y=3x与反比例函数y= 的图象于点E,F。①当t= 时,求线段EF的长;
②若0<EF≤8,请根据图象直接写出t的取值范围。
22. 如图,在等腰△ABC中,AC=BC= ,AB=6,点E从点B沿着射线BA以每秒3个单位的速度运动,过点E作BC的平行线交∠ACB的外角平分线CF于点F。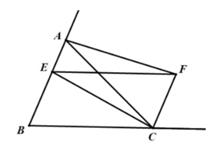 (1)、求证:四边形BCFE是平行四边形;(2)、当点E是边AB的中点时,连结AF,试判断四边形AECF的形状,并说明理由;(3)、设运动时间为t秒,是否存在t的值,使得以△EFC的其中两边为邻边所构造的平行四边形恰好是菱形?若存在,请求出t的值;若不存在,试说明理由。
(1)、求证:四边形BCFE是平行四边形;(2)、当点E是边AB的中点时,连结AF,试判断四边形AECF的形状,并说明理由;(3)、设运动时间为t秒,是否存在t的值,使得以△EFC的其中两边为邻边所构造的平行四边形恰好是菱形?若存在,请求出t的值;若不存在,试说明理由。