山东省济南市商河县2018-2019学年九年级上学期数学期中考试试卷

试卷更新日期：2019-09-29 类型：期中考试

进入出卷网下载

一、单选题

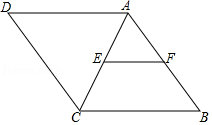
1. 菱形不具备的性质是（）

A、四条边都相等 B、对角线一定相等 C、是轴对称图形 D、是中心对称图形

查看试题解析
2. 如图，在菱形ABCD中，E是AC的中点，EF∥CB，交AB于点F，如果EF=3，那么菱形ABCD的周长为（）

A、24 B、18 C、12 D、9

查看试题解析
3. 一元二次方程 $y^{2} - y - \frac{3}{4} = 0$ 配方后可化为（）

A、 ${(y + \frac{1}{2})}^{2} = 1$ B、 ${(y - \frac{1}{2})}^{2} = 1$ C、 ${(y + \frac{1}{2})}^{2} = \frac{3}{4}$ D、 ${(y - \frac{1}{2})}^{2} = \frac{3}{4}$

查看试题解析
4. 若2- $\sqrt{3}$ 是方程x²-4x+c=0的一个根，则c的值是（）

A、1 B、3- $\sqrt{3}$ C、1+ $\sqrt{3}$ D、2+ $\sqrt{3}$

查看试题解析
5. 如图，某小区计划在一块长为32m，宽为20m的矩形空地上修建三条同样宽的道路，剩余的空地上种植草坪，使草坪的面积为570m² ．若设道路的宽为xm，则下面所列方程正确的是（）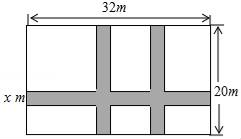

A、（32﹣2x）（20﹣x）=570 B、32x+2×20x=32×20﹣570 C、（32﹣x）（20﹣x）=32×20﹣570 D、32x+2×20x﹣2x²=570

查看试题解析
6. 已知关于x的一元二次方程x²-2x+k-1=0有两个不相等的实数根，则实数 $k$ 的取值范围是（）

A、k≤2 B、k≤0 C、k<2 D、k<0

查看试题解析
7. 方程3x（x﹣1）＝4（x﹣1）的根是（）

A、 $\frac{4}{3}$ B、1 C、 $\frac{4}{3}$ 和1 D、 $\frac{4}{3}$ 和﹣1

查看试题解析
8. 一个不透明的盒子中放入四张卡片，每张卡片上都写有一个数字，分别为﹣2，﹣1，0，1．卡片除数字不同外其他都相同，从中随机抽取两张卡片，其数字之和为负数的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
9. 如图，矩形ABCD中， $AB = 3$ ， $BC = 4$ ， $EB / / DF$ 且BE与DF之间的距离为3，则AE的长是 $($ ）

A、 $\sqrt{7}$ B、 $\frac{3}{8}$ C、 $\frac{7}{8}$ D、 $\frac{5}{8}$

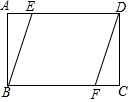查看试题解析
10. 如图，小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC相似的是（）

A、 B、 C、 D、

查看试题解析
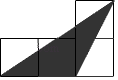11. 如图，在平行四边形ABCD中，E是DC上的点，DE：EC=3：2，连接AE交BD于点F，则△DEF与△BAF的面积之比为（）

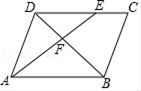A、2：5 B、3：5 C、9：25 D、4：25

查看试题解析
12. 如图，正方形ABCD的对角线AC与BD相交于点O ， ∠ACB的平分线分别交AB、BD于点M、N ，若AD＝4，则线段AM的长为（）

A、2 B、2 $\sqrt{2}$ C、4﹣ $\sqrt{2}$ D、8﹣4 $\sqrt{2}$

查看试题解析

二、填空题

13. 原价100元的某商品，连续两次降价后售价为81元，若每次降低的百分率相同，则降低的百分率为．

查看试题解析
14. 已知一个菱形的边长为2，较长的对角线长为2 $\sqrt{3}$ ，则这个菱形的面积是．

查看试题解析
15. 一个三角形的两边长分别为3和6，第三边长是方程x²-10x+21=0的根，则三角形的周长为.

查看试题解析
16. 在不透明的口袋中有若干个完全一样的红色小球，现放入10个仅颜色不同的白色小球，均匀混合后，有放回的随机摸取30次，有10次摸到白色小球，据此估计该口袋中原有红色小球个数为．

查看试题解析
17. 如图，已知矩形ABCD的顶点A、D分别落在x轴、y轴，OD＝2OA＝6，AD：AB＝3：1．则点B的坐标是．

查看试题解析
18. 如图，在平行四边形ABCD中，AB＝12，AD＝8，∠ABC的平分线交CD于点F ，交AD的延长线于点E ， CG⊥BE ，垂足为G ，若EF＝2，则线段CG的长为．

查看试题解析

三、解答题

19. 解方程：3x²﹣2x﹣2＝0．

查看试题解析
20. 如图，在矩形ABCD，AD＝AE，DF⊥AE于点F．求证：AB＝DF．

查看试题解析
21. 如图，小强自制了一个小孔成像装置，其中纸筒的长度为15cm ，他准备了一支长为20cm的蜡烛，想要得到高度为5cm的像，蜡烛应放在距离纸筒多远的地方？

查看试题解析
22. 如图，在 $▱$ ABCD中，AE⊥BC，AF⊥CD，垂足分别为E、F，且BE=DF。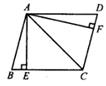

(1)、求证： $▱$ ABCD是菱形；

(2)、若AB=5，AC=6，求 $▱$ ABCD的面积。

查看试题解析
23. 一商店销售某种商品，平均每天可售出20件，每件盈利40元.为了扩大销售、增加盈利，该店采取了降价措施，在每件盈利不少于25元的前提下，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件.

(1)、若降价3元，则平均每天销售数量为件；

(2)、当每件商品降价多少元时，该商店每天销售利润为1200元？

查看试题解析
24. 在一个不透明的布袋里装有4个标有1、2、3、4的小球，它们的形状、大小完全相同，李强从布袋中随机取出一个小球，记下数字为x，王芳在剩下的3个小球中随机取出一个小球，记下数字为y，这样确定了点M的坐标 $(x ， y)$

(1)、画树状图列表，写出点M所有可能的坐标；

(2)、求点 $M (x ， y)$ 在函数 $y = x + 1$ 的图象上的概率．

查看试题解析
25. 如图，正方形ABCD中，M为BC上一点，F是AM的中点，EF⊥AM，垂足为F，交AD的延长线于点E，交DC于点N．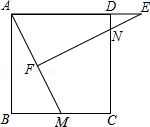

(1)、求证：△ABM∽△EFA；

(2)、若AB=12，BM=5，求DE的长．

查看试题解析
26. 如图，在矩形ABCD中，AB＝12厘米，BC＝6厘米，点P沿AB边从点A开始向点B以2厘米/秒的速度移动，点Q沿DA边从点D开始向点A以1厘米/秒的速度移动，如果点P、Q同时出发，用t（秒）表示移动的时间（0≤t≤6）．

(1)、当PB＝2厘米时，求点P移动多少秒？

(2)、t为何值时，△PAQ为等腰直角三角形？

(3)、求四边形QAPC的面积，并探究一个与计算结果有关的结论．

查看试题解析
27. 如图

(1)、（操作发现）：如图一，在矩形ABCD中，E是BC的中点，将△ABE沿AE折叠后得到△AFE ，点F在矩形ABCD内部，延长AF交CD于点G ．猜想线段GF与GC的数量关系是

(2)、（类比探究）：如图二，将（1）中的矩形ABCD改为平行四边形，其它条件不变，（1）中的结论是否仍然成立？请说明理由．

(3)、（应用）：如图三，将（1）中的矩形ABCD改为正方形，边长AB＝4，其它条件不变，求线段GC的长．

查看试题解析