江西省丰城市2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期:2019-09-29 类型:期中考试
一、单选题
-
1. 下列方程中,一定是关于x的一元二次方程的是( )A、 B、 C、 D、2. 抛物线y=(x+2)2﹣3可以由抛物线y=x2平移得到,则下列平移过程正确的是( )A、先向左平移2个单位,再向上平移3个单位 B、先向左平移2个单位,再向下平移3个单位 C、先向右平移2个单位,再向下平移3个单位 D、先向右平移2个单位,再向上平移3个单位3. 关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根是0,则a的值是( )A、﹣1 B、1 C、1或﹣1 D、﹣1或04. 如图,以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C,D为第一象限内 上的一点,若 ,则 的度数是
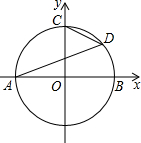 A、 B、 C、 D、5. 如图,将 绕直角顶点C顺时针旋转 ,得到 ,连接 ,若 ,则 的度数是 )
A、 B、 C、 D、5. 如图,将 绕直角顶点C顺时针旋转 ,得到 ,连接 ,若 ,则 的度数是 ) A、 B、 C、 D、6. 欧几里得的《原本》记载,形如 的方程的图解法是:画 ,使 , , ,再在斜边 上截取 .则该方程的一个正根是( )
A、 B、 C、 D、6. 欧几里得的《原本》记载,形如 的方程的图解法是:画 ,使 , , ,再在斜边 上截取 .则该方程的一个正根是( )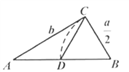 A、 的长 B、 的长 C、 的长 D、 的长
A、 的长 B、 的长 C、 的长 D、 的长二、填空题
-
7. 若m是方程2x2-3x-1=0的一个根,则6m2-9m+2015的值为 .8. 已知开口向上的抛物线 ,在此抛物线上有 , 和 三点,则 , 和 的大小关系为 .9. 如图,CD是 的直径,弦 于点E,若 ,CE: :9,则 的半径是 .
 10. 如图,正方形ABCD的边长为3,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上,将正方形ABCD绕点A逆时针旋转 至正方形 的位置, 与CD相交于点M,则点M的坐标为 .
10. 如图,正方形ABCD的边长为3,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上,将正方形ABCD绕点A逆时针旋转 至正方形 的位置, 与CD相交于点M,则点M的坐标为 .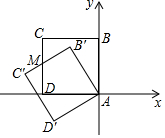 11. 如图, 经过正六边形ABCDEF的顶点A、E,则弧AE所对的圆周角 等于.
11. 如图, 经过正六边形ABCDEF的顶点A、E,则弧AE所对的圆周角 等于.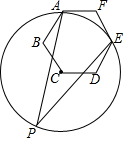 12. 小颖从如图所示的二次函数 的图象中,观察得出了下列信息: ; ; ; ; .你认为其中错误信息的个数有 .
12. 小颖从如图所示的二次函数 的图象中,观察得出了下列信息: ; ; ; ; .你认为其中错误信息的个数有 .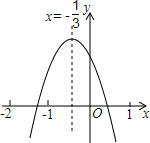
三、解答题
-
13. 解方程:①
②
14. 抛物线的顶点坐标为 ,且与y轴的交点为 ,求此抛物线的解析式.15. 如图,在平面直角坐标系中,已知点 , 轴于A. (1)、画出将 绕原点顺时针旋转 后所得的 ,并写出点 、 的坐标;(2)、画出 关于原点O的中心对称图形 ,并写出点 、 的坐标.16. 如图,已知正三角形ABC内接于 ,AD是 的内接正十二边形的一条边长,连接CD,若 ,求 的半径.
(1)、画出将 绕原点顺时针旋转 后所得的 ,并写出点 、 的坐标;(2)、画出 关于原点O的中心对称图形 ,并写出点 、 的坐标.16. 如图,已知正三角形ABC内接于 ,AD是 的内接正十二边形的一条边长,连接CD,若 ,求 的半径.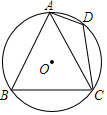 17.
17.作图题:在⊙O 中,点D是劣弧AB的中点,仅用无刻度的直尺画线的方法,按要求完下列作图:
在图(1)中作出∠C的平分线;在图(2)中画一条弦,平分△ABC的面积.
 18. 已知关于x的方程x2-(k+2)x+2k=0.(1)、求证:k取任何实数值,方程总有实数根;(2)、若Rt△ABC斜边长a=3,另两边长b,c恰好是这个方程的两个根,求△ABC的周长.19. 如图,某单向行驶隧道横截面上的上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成.矩形的长是12米,宽是3米,隧道的最大高度为6米,现以O点为原点,OM所在直线为x轴建立直角坐标系.
18. 已知关于x的方程x2-(k+2)x+2k=0.(1)、求证:k取任何实数值,方程总有实数根;(2)、若Rt△ABC斜边长a=3,另两边长b,c恰好是这个方程的两个根,求△ABC的周长.19. 如图,某单向行驶隧道横截面上的上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成.矩形的长是12米,宽是3米,隧道的最大高度为6米,现以O点为原点,OM所在直线为x轴建立直角坐标系.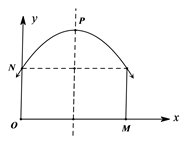 (1)、直接写出点M、点N及抛物线顶点P的坐标;(2)、求出这条抛物线的函数解析式;(3)、一大货运汽车装载某大型设备后高为5米,宽为4米,那么这辆货车能否安全通过?20. 如图,已知⊙O的直径CD=6,A,B为圆周上两点,且四边形OABC是平行四边形。过A点作直线EF∥BD,分别交CD,CB的延长线于点E,F,AO与BD交于G点.
(1)、直接写出点M、点N及抛物线顶点P的坐标;(2)、求出这条抛物线的函数解析式;(3)、一大货运汽车装载某大型设备后高为5米,宽为4米,那么这辆货车能否安全通过?20. 如图,已知⊙O的直径CD=6,A,B为圆周上两点,且四边形OABC是平行四边形。过A点作直线EF∥BD,分别交CD,CB的延长线于点E,F,AO与BD交于G点.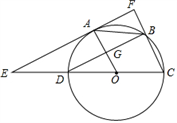 (1)、求证:EF是⊙O的切线;(2)、求AE的长.21. 将两个全等的直角三角形ABC和DBE按图 方式摆放,其中 , ,点E落在AB上,DE所在直线交AC所在直线于点F.
(1)、求证:EF是⊙O的切线;(2)、求AE的长.21. 将两个全等的直角三角形ABC和DBE按图 方式摆放,其中 , ,点E落在AB上,DE所在直线交AC所在直线于点F.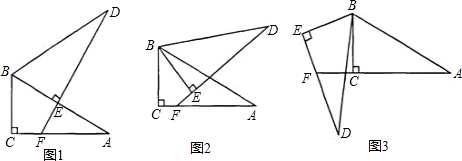 (1)、求证: ;(2)、若将图 中的 绕点B按顺时针方向旋转角a,且 ,其他条件不变,如图 请你直接写出 与DE的大小关系: 填“ ”或“ ”或“ ”(3)、若将图 中 的绕点B按顺时针方向旋转角 ,且 ,其他条件不变,如图 请你写出此时AF、EF与DE之间的关系,并加以证明.22. 在平面直角坐标系中,已知抛物线经过 , , 三点.
(1)、求证: ;(2)、若将图 中的 绕点B按顺时针方向旋转角a,且 ,其他条件不变,如图 请你直接写出 与DE的大小关系: 填“ ”或“ ”或“ ”(3)、若将图 中 的绕点B按顺时针方向旋转角 ,且 ,其他条件不变,如图 请你写出此时AF、EF与DE之间的关系,并加以证明.22. 在平面直角坐标系中,已知抛物线经过 , , 三点.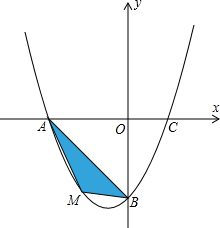 (1)、求抛物线的解析式;(2)、若点M为第三象限内抛物线上一动点,点M的横坐标为m, 的面积为S.求S关于m的函数关系式,并求出S的最大值.(3)、若点P是抛物线上的动点,点Q是直线 上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
(1)、求抛物线的解析式;(2)、若点M为第三象限内抛物线上一动点,点M的横坐标为m, 的面积为S.求S关于m的函数关系式,并求出S的最大值.(3)、若点P是抛物线上的动点,点Q是直线 上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.