北京市朝阳区2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期：2019-09-29 类型：期中考试
一、单选题
-
1. 以下是回收、绿色包装、节水、低碳四个标志，其中是中心对称图形的是（ ）A、
B、
C、
D、
2. 二次函数y＝（x+2）2+3的图象的顶点坐标是（ ）A、（﹣2，3） B、（2，3） C、（﹣2，﹣3） D、（2，﹣3）3. 如图，⊙O的直径为10，AB为弦，OC⊥AB ， 垂足为C ， 若OC＝3，则弦AB的长为（ ）
A、8 B、6 C、4 D、104. 如图，AB是⊙O的直径，CD是⊙O的弦，∠ABD＝59°，则∠C等于（ ）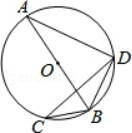
A、29° B、31° C、59° D、62°5. 如图4×4的正方形网格中，△PMN绕某点旋转一定的角度，得到△P1M1N1 ， 其旋转中心是（ ）
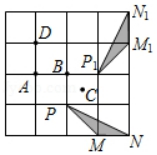A、A点 B、B点 C、C点 D、D点6. 如图，AB是⊙O的直径，弦CD⊥AB ， ∠CDB＝30°，CD＝6，阴影部分图形的面积为（ ）
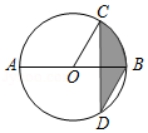A、4π B、3π C、2π D、π7. 已知抛物线y＝ax2+bx+c上部分点的横坐标x纵坐标y的对应值如下表：X
……
﹣1
0
1
2
3
……
Y
……
3
0
﹣1
0
3
①物线y＝ax2+bx+c的开口向下；②抛物线y＝ax2+bx+c的对称轴为直线x＝﹣1；③方程ax2+bx+c＝0的根为0和2；④当y＞0时，x的取值范围是x＜0或x＞2以上结论中其中的是（ ）
A、①④ B、②④ C、②③ D、③④8. 如图1，⊙O过正方形ABCD的顶点A、D且与边BC相切于点E ， 分别交AB、DC于点M、N ． 动点P在⊙O或正方形ABCD的边上以每秒一个单位的速度做连续匀速运动．设运动的时间为x ， 圆心O与P点的距离为y ， 图2记录了一段时间里y与x的函数关系，在这段时间里P点的运动路径为（ ）
A、从D点出发，沿弧DA→弧AM→线段BM→线段BC B、从B点出发，沿线段BC→线段CN→弧ND→弧DA C、从A点出发，沿弧AM→线段BM→线段BC→线段CN D、从C点出发，沿线段CN→弧ND→弧DA→线段AB二、填空题
-
9. 在平面直角坐标系中，点P（2，﹣3）关于原点对称点P′的坐标是 ．10. 平面直角坐标系xOy中，以原点O为圆心，5为半径作⊙O ， 则点A（4，3）在⊙O（填：“内”或“上“或“外”）11. 如图所示，把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转，使得点A落在CB的延长线上的点E处，则∠BDC的度数为度．
12. 将抛物线y＝x2﹣6x+5化成y＝a（x﹣h）2﹣k的形式，则hk＝ ．13. 若正六边形的边长为2，则其外接圆的面积为 ．14. 二次函数满足下列条件：①函数有最大值3；②对称轴为y轴，写出一个满足以上条件的二次函数解析式：15. 圆锥底面半径为6，高为8，则圆锥的侧面积为 ．16. 阅读下面材料：在数学课上，老师提出利用尺规作图完成下面问题：
已知：∠ACB是△ABC的一个内角．
求作：∠APB＝∠ACB ．
小明的做法如下：
如图
①作线段AB的垂直平分线m；
②作线段BC的垂直平分线n ， 与直线m交于点O；
③以点O为圆心，OA为半径作△ABC的外接圆；
④在弧ACB上取一点P ， 连结AP ， BP ．
所以∠APB＝∠ACB ．
老师说：“小明的作法正确．”
请回答：
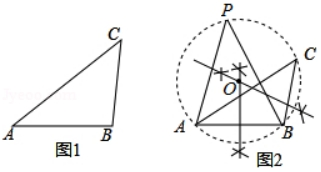(1)、点O为△ABC外接圆圆心（即OA＝OB＝OC）的依据是；(2)、∠APB＝∠ACB的依据是 ．三、解答题
-
17. 如图，在Rt△OAB中，∠OAB＝90，且点B的坐标为（4，2）
(1)、画出△OAB绕点O逆时针旋转90°后的△OA1B1 ．(2)、求点B旋转到点B1所经过的路线长（结果保留π）18. 二次函数y＝ax2+bx+c（a≠0）的部分图象如图所示．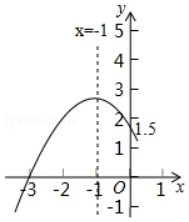
(1)、确定二次函数的解析式；(2)、若方程ax2+bx+c＝k有两个不相等的实数根，求k的取值范围．19. 如图，四边形ABCD内接于⊙O ， ∠ABC＝135°，AC＝4，求⊙O的半径长．
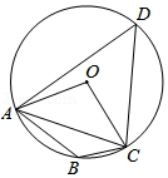20. 关于x一元二次方程x2+mx+n＝0．(1)、当m＝n+2时，利用根的判别式判断方程根的情况．(2)、若方程有实数根，写出一组满足条件的m ， n的值，并求此时方程的根．21. 如图，PA，PB是⊙O的切线，点A，B为切点，AC是⊙O的直径，∠ACB=70°，求∠APB的度数.
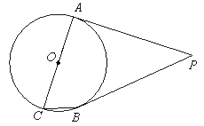22. 某商店销售一种进价为20元/双的手套，经调查发现，该种手套每天的销售量w（双）与销售单价x（元）满足w＝﹣2x+80（20≤x≤40），设销售这种手套每天的利润为y（元）．(1)、求y与x之间的函数关系式；(2)、当销售单价定为多少元时，每天的利润最大？最大利润是多少？23. 如图，已知直角坐标系中一条圆弧经过正方形网格的格点A（0，4）、B（4，4）、C（6，2）
(1)、用直尺画出该圆弧所在圆的圆心M的位置，并标出M点的坐标；(2)、若D点的坐标为（7，0），想一想直线CD与⊙M有怎样的位置关系，并证明你的猜想．24. 已知：如图，在△ABC中，AB＝AC ， 以AC为直径的⊙O与BC交于点D ， DE⊥AB ， 垂足为E ， ED的延长线与AC的延长线交于点F ．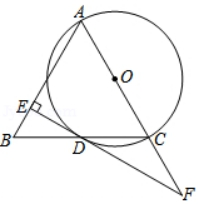
(1)、求证：DE是⊙O的切线；(2)、若⊙O的半径为4，∠F＝30°，求DE的长．25. 如图，Q是弧AB与弦AB所围成的图形的内部的一定点，P是弦AB上一动点，连接PQ并延长交弧AB于点C ， 连接BC ． 已知AB＝6cm ， 设A ， P两点间的距离为xcm ， P ， C两点间的距离为y1cm ， A ， C两点间的距离为y2cm ．
小明根据学习函数的经验，分别对函数y1 ， y2 ， 随自变量x的变化而变化的规律进行了探究．
下面是小明的探究过程，请补充完整：
(1)、确定自变量x的取值范围是 ．(2)、按下表中自变量x的值进行取点、画图、测量，分别得到了y1 ， y2与x的几组对应值．x/cm
0
1
2
3
4
5
6
y1/cm
5.62
4.67
3.76
2.65
3.18
4.37
y2/cm
5.62
5.59
5.53
5.42
5.19
4.73
4.11
(3)、在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点（x ， y1），（x ， y2），并面出函数y1 ， y2的图象．(4)、结合函数图象，解决问题：当△APC为等腰三角形时，AP的长度约为cm ．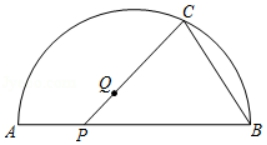
26. 在平面直角坐标系中xOy中，抛物线y＝x2﹣4x+m+2的顶点在x轴上．
(1)、求抛物线的表达式；(2)、点Q是x轴上一点，①若在抛物线上存在点P ， 使得∠POQ＝45°，求点P的坐标．
②抛物线与直线y＝1交于点E ， F（点E在点F的左侧），将此抛物线在点E ， F（包含点E和点F）之间的部分沿x轴向左平移n个单位后得到的图象记为G ， 若在图象G上存在点P ， 使得∠POQ＝45°，求n的取值范围．
27. 已知：在四边形ABCD中，AB＝AD ， ∠ABC+∠ADC＝180°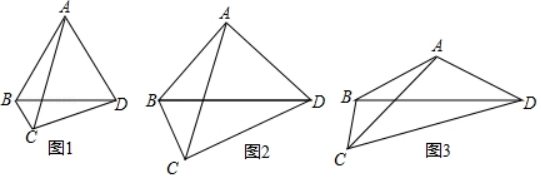
(1)、如图①，若∠ACD＝60°，BC＝1，CD＝3，则AC的长为；(2)、如图②，若∠ACD＝45°，BC＝1，CD＝3，求出AC的长；(3)、如图③，若∠ACD＝30°，BC＝a ， CD＝b ， 直接写出AC的长．28. 在平面直角坐标系xOy中，点A的坐标为（0，m），且m≠0，点B的坐标为（n ， 0），将线段AB绕点B顺时针旋转90°．得到线段BA1 ， 称点A1为点A关于点B的“伴随点”，图1为点A关于点B的“伴随点”的示意图
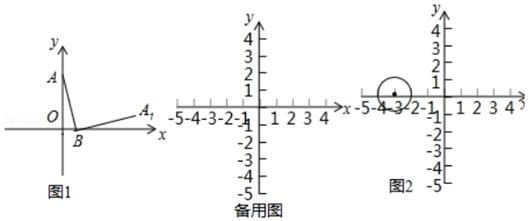(1)、已知点A（0，4），①当点B的坐标分别为（1，0），（﹣2，0）时，点A关于点B的“伴随点”的坐标分别为 ， ；
(2)、②点（x ， y）是点A关于点B的“伴随点”，直接写出y与x之间的关系式；
(3)、如图2，点C的坐标为（﹣3，0），以C为圆心， 为半径作圆，若在⊙C上存在点A关于点B的“伴随点”，直接写出点A的纵坐标m的取值范围．