山东省东营胜利油田2018-2019学年九年级上学期数学期中考试试卷

试卷更新日期：2019-09-29 类型：期中考试

进入出卷网下载

一、单选题

1. $\sqrt{16}$ 的算术平方根是（）

A、±2 B、2 C、±4 D、4

查看试题解析
2. 下列计算正确的是（）

A、2a•3b＝5ab B、a³•a⁴＝a¹² C、（﹣3a²b）²＝6a⁴b² D、a⁵÷a³+a²＝2a²

查看试题解析
3. 下列说法正确的有（）

A、正整数、正分数、和0统称为有理数 B、正整数、负整数统称为有理数 C、正有理数、负有理数和0统称有理数 D、0不是有理数

查看试题解析
4. 把一块直尺与一块三角板如图放置，若∠2=130°，则∠1的度数为（）

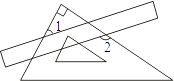A、30° B、35° C、40° D、45°

查看试题解析
5. 下列说法不一定成立的是（）

A、若a>b，则a+c>b+c B、若a+c>b+c，则a>b C、若a>b，则ac²>bc² D、若ac²>bc² ，则a>b

查看试题解析
6. 如图，在平行四边形ABCD中，E是DC上的点，DE：EC=3：2，连接AE交BD于点F，则△DEF与△BAF的面积之比为（）

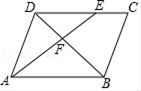A、2：5 B、3：5 C、9：25 D、4：25

查看试题解析
7. 一商店以每件150元的价格卖出两件不同的商品，其中一件盈利25%，另一件亏损25%，则商店卖这两件商品总的盈亏情况是（）

A、亏损20元 B、盈利30元 C、亏损50元 D、不盈不亏

查看试题解析
8. 在一次数学测验中，随机抽取了10份试卷，其成绩如下：85，81，89，81，72，82，77，81，79，83，则这组数据的中位数为（）

A、72 B、81 C、77 D、82

查看试题解析
9. 关于x的分式方程 $\frac{2 x + a}{x + 1} = 1$ 的解为负数，则a的取值范围是（）

A、 $a > 1$ B、 $a < 1$ C、 $a < 1$ 且 $a \neq - 2$ D、 $a > 1$ 且 $a \neq 2$

查看试题解析
10. 如图，在△ABC中∠A=60°，BM⊥AC于点M，CN⊥AB于点N，P为BC边的中点，连接PM，PN，则下列结论：①PM=PN；② $\frac{A M}{A B} = \frac{A N}{A C}$ ；③△PMN为等边三角形；④当∠ABC=45°时，BN= $\sqrt{2}$ PC．其中正确的个数是（）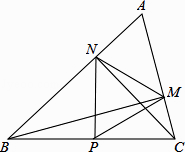

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 讲究卫生要勤洗手，人的一只手上大约有28 000万个看不见的细菌，用科学记数法表示一只手上大约有个细菌.

查看试题解析
12. 因式分解：x²y﹣y³＝．

查看试题解析
13. 如图，在平面直角坐标系中，A（4，0），B（0，3），以点A为圆心，AB长为半径画弧，交x轴的负半轴于点C，则点C坐标为．

查看试题解析
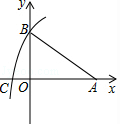14. 已知圆锥的底面半径是3，高是4，则这个圆锥的全面积是.

查看试题解析
15. 如图，∠BAC=30°，M为AC上一点，AM=2，点P是AB上的一动点，PQ⊥AC ，垂足为点Q ，则PM+PQ的最小值为．

查看试题解析
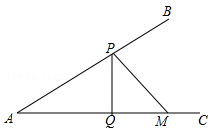16. 网格中的每个小正方形的边长都是1，△ABC每个顶点都在网格的交点处，则sinA= ．

查看试题解析
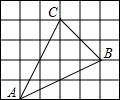17. 《孙子算经》是中国古代重要的数学著作，成书于约一千五百年前，其中有首歌谣：“今有竿不知其长，量得影长一丈五尺，立一标杆，长一尺五寸，影长五寸，问竿长几何？”意思就是：有一根竹竿不知道有多长，量出它在太阳下的影子长一丈五尺，同时立一根一尺五寸的小标杆（如图所示），它的影长五寸（提示：1丈＝10尺，1尺＝10寸），则竹竿的长为．

查看试题解析
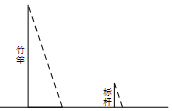18. 如图，AB⊥y轴，垂足为B，将△ABO绕点A逆时针旋转到△AB₁O₁的位置，使点B的对应点B₁落在直线y=﹣ $\frac{\sqrt{3}}{3}$ x上，再将△AB₁O₁绕点B₁逆时针旋转到△A₁B₁O₂的位置，使点O₁的对应点O₂落在直线y=﹣ $\frac{\sqrt{3}}{3}$ x上，依次进行下去…若点B的坐标是（0，1），则点O₂₀₂₀的纵坐标为．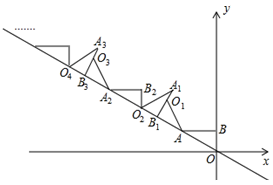

查看试题解析

三、解答题

19.

(1)、计算：|﹣ $\sqrt{3}$ |﹣ $\sqrt{12}$ +2sin60°+（ $\frac{1}{3}$ ）^﹣¹+（2﹣ $\sqrt{3}$ ）⁰

(2)、先化简，再求值： $\frac{a}{a^{2} + 4 a + 4}$ ÷（1﹣ $\frac{2 a - 4}{a^{2} - 4}$ ），其中a= $\sqrt{3}$ ﹣2．

查看试题解析

20. 某区规定学生每天户外体育活动时间不少于1小时．为了解学生参加户外体育活动的情况，对部分学生每天参加户外体育活动的时间进行了随机抽样调查，并将调查结果绘制成如下的统计表（不完整）．

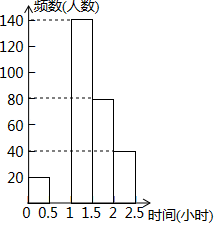
组别	时间（小时）	频数（人数）	频率
A	0≤t＜0.5	20	0.05
B	0.5≤t＜1	a	0.3
C	1≤t＜1.5	140	0.35
D	1.5≤t＜2	80	0.2
E	2≤t＜2.5	40	0.1

请根据图表中的信息，解答下列问题：

(1)、表中的a= ，将频数分布直方图补全；

(2)、该区8000名学生中，每天户外体育活动的时间不足1小时的学生大约有多少名？

(3)、若从参加户外体育活动时间最长的3名男生和1名女生中随机抽取两名，请用画树状图或列表法求恰好抽到1名男生和1名女生的概率．

查看试题解析

21. 如图，在Rt△ABC中， $∠ C = 90 °$ ，AD平分∠BAC，交BC于点D，点O在AB上，⊙O经过A、D两点，交AC于点E，交AB于点F．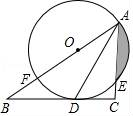

(1)、求证：BC是⊙O的切线；

(2)、若⊙O的半径是2cm，E是弧AD的中点，求阴影部分的面积（结果保留π和根号）

查看试题解析
22. 某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克，大樱桃的进价比小樱桃的进价每千克多20元．大樱桃售价为每千克40元，小樱桃售价为每千克16元。

(1)、大樱桃和小樱桃的进价分别是每千克多少元？销售完后，该水果商共赚了多少元钱?

(2)、该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克，进价不变，但在运输过程中小樱桃损耗了20%．若小樱桃的售价不变，要想让第二次赚的钱不少于第一次所赚钱的90%，大樱桃的售价最少应为多少?

查看试题解析
23. 如图，在平面直角坐标系中，A点的坐标为（a，6），AB⊥x轴于点B，cos∠OAB═ $\frac{3}{5}$ ，反比例函数y= $\frac{k}{x}$ 的图象的一支分别交AO、AB于点C、D．延长AO交反比例函数的图象的另一支于点E．已知点D的纵坐标为 $\frac{3}{2}$ ．

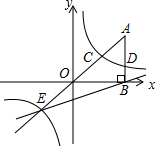(1)、求反比例函数的解析式；

(2)、求直线EB的解析式；

(3)、求S_△_OEB ．

查看试题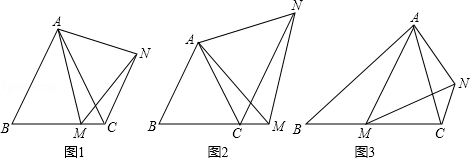解析
24. 如图

（提出问题）

(1)、如图1，在等边△ABC中，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等边△AMN，连结CN．求证：∠ABC=∠ACN．

(2)、如图2，在等边△ABC中，点M是BC延长线上的任意一点（不含端点C），其它条件不变，（1）中结论∠ABC=∠ACN还成立吗？请说明理由．

(3)、如图3，在等腰△ABC中，BA=BC，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等腰△AMN，使顶角∠AMN=∠ABC．连结CN．试探究∠ABC与∠ACN的数量关系，并说明理由．

查看试题解析
25. 如图，在平面直角坐标系中，抛物线y=ax²+2x+c与x轴交于A（﹣1，0）B（3，0）两点，与y轴交于点C，点D是该抛物线的顶点．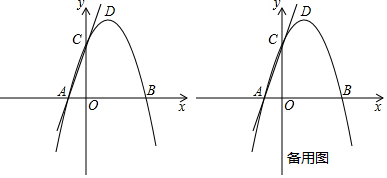

(1)、求抛物线的解析式和直线AC的解析式；

(2)、请在y轴上找一点M，使△BDM的周长最小，求出点M的坐标；

(3)、试探究：在拋物线上是否存在点P，使以点A，P，C为顶点，AC为直角边的三角形是直角三角形？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．

查看试题解析