北京市朝阳区垂杨柳片区2018-2019学年七年级上学期数学期中考试试卷

试卷更新日期：2019-09-29 类型：期中考试

进入出卷网下载

一、单选题

1. 由美国主题景点协会（TEA）和国际专业技术与管理咨询服务提供商AECOM的经济部门合作撰写的2016年《主题公园指数和博物馆指数报告》中显示，中国国家博物馆以7550000的参观人数拔得头筹，成为全世界人气最旺、最受欢迎的博物馆．请将7550000用科学记数法表示为（）

A、755×10⁴ B、75.5×10⁵ C、7.55×10⁶ D、0.755×10⁷

查看试题解析
2. 下列各式中结果为负数的是（）

A、﹣（﹣2） B、|﹣2| C、（﹣2）² D、﹣2²

查看试题解析
3. 比 $- 4.5$ 大的负整数有（）

A、3个 B、4个 C、5个 D、无数个

查看试题解析
4. 已知x＝﹣2是方程x+4a＝10的解，则a的值是（）

A、3 B、 $\frac{1}{2}$ C、2 D、﹣3

查看试题解析
5. 下列计算正确的是（）

A、3x²﹣x²＝3 B、﹣3a²﹣2a²＝﹣a² C、3（a﹣1）＝3a﹣1 D、﹣2（x+1）＝﹣2x﹣2

查看试题解析
6. 如果x＝y，那么根据等式的性质下列变形正确的是（）

A、x+y＝0 B、 $\frac{1}{3}$ x＝ $\frac{1}{2}$ y C、2﹣x＝2﹣y D、x+7＝y﹣7

查看试题解析
7. 小静喜欢逛商场，某天小静看到某商场举行促销活动，促销的方法是“消费超过1000元时，所购买的商品按原价打8折后，再减少100元”．若某商品的原价为x元（x＞1000），则购买该商品实际付款的金额（单位：元）是（）

A、80%x﹣100 B、80%（x﹣100） C、20%（x﹣100） D、20%x﹣100

查看试题解析
8. 如图所示，数轴上点A、B对应的有理数分别为a、b，下列说法正确的是（）
①a＜0＜b②|a|＜|b|③ab＞0 ④b﹣a＞a+b

A、①② B、①④ C、②③ D、③④

查看试题解析

二、填空题

9. 单项式 $- \frac{3 x^{2} y}{4}$ 的系数是，次数是．

查看试题解析
10. 用四舍五入法，将4.7893取近似数并精确到十分位，得到的数为．

查看试题解析
11. 小何买了4本笔记本，10支圆珠笔，设笔记本的单价为a元，圆珠笔的单价为b元，则小何共花费元．（用含a，b的代数式表示）

查看试题解析
12. 已知a，b满足|a﹣2|+（b+3）²＝0，那么a＝， b＝．

查看试题解析
13. 若一个多项式与m﹣2n的和等于2m，则这个多项式是．

查看试题解析
14. 如图所示的框图表示解方程3﹣5x=4﹣2x的流程，其中“系数化为1”这一步骤的依据是．

查看试题解析
15. 按下面程序计算，若开始输入x的值为正数，最后输出的结果为656，则满足条件所有x的值是．

查看试题解析

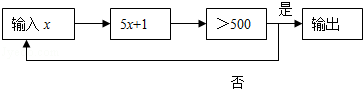
三、解答题

16. 计算：（﹣ $\frac{1}{2}$ ）×（﹣8）+（﹣6）² ．

查看试题解析
17. 计算：﹣1⁴+（﹣2）÷（﹣ $\frac{1}{3}$ ）﹣|﹣9|．

查看试题解析
18. 计算4a﹣2b+3（3b﹣2a）．

查看试题解析
19. 化简：5x²y﹣2xy﹣4（x²y﹣ $\frac{1}{2}$ xy）

查看试题解析
20. 解方程：7+2x＝12﹣2x．

查看试题解析
21. 解方程：x﹣3＝﹣ $\frac{1}{2}$ x﹣4．

查看试题解析
22. 先化简，再求值： $(7 x^{2} - 3 x y) - 6 (x^{2} - \frac{1}{3} x y)$ ，其中x＝﹣3，y＝ $\frac{1}{3}$ ．

查看试题解析
23. 已知x²﹣2y﹣5＝0，求3（x²﹣2xy）﹣（x²﹣6xy）﹣4y的值．

查看试题解析
24. 之前我们学习了一元一次方程的解法，下面是一道解一元一次方程的题：
解方程 $\frac{2 - 3 x}{3}$ ﹣ $\frac{x - 5}{2}$ ＝1

老师说：这是一道含有分母的一元一次方程，我们可以根据等式的性质，可以把方程的两边同乘以6，这样就可以去掉分母了．于是，小明按照老师说的方法进行了解答，小明同学的解题过程如下：

解：方程两边同时乘以6，得 $\frac{2 - 3 x}{3}$ ×6﹣ $\frac{x - 5}{2}$ ×6＝1…………①

去分母，得：2（2﹣3x）﹣3（x﹣5）＝1………②

去括号，得：4﹣6x﹣3x+15＝1……………③

移项，得：﹣6x﹣3x＝1﹣4﹣15…………④

合并同类项，得﹣9x＝﹣18……………⑤

系数化1，得：x＝2………………⑥

(1)、上述小明的解题过程从第步开始出现错误，错误的原因是．

(2)、请帮小明改正错误，写出完整的解题过程．

查看试题解析
25. 对于任意有理数a，b，定义运算：a⊙b＝a（a+b）﹣1，等式右边是通常的加法、减法、乘法运算，例如，2⊙5＝2×（2+5）﹣1＝13；（﹣3）⊙（﹣5）＝﹣3×（﹣3﹣5）﹣1＝23．

(1)、求（﹣2）⊙3 $\frac{1}{2}$ 的值；

(2)、对于任意有理数m，n，请你重新定义一种运算“⊕”，使得5⊕3＝20，写出你定义的运算：m⊕n＝（用含m，n的式子表示）．

查看试题解析
26. 小兵喜欢研究数学问题，在计算整式的加减（﹣4x²﹣7+5x）+（2x﹣3+3x²）的时候，想到了小学的列竖式加减法，令A＝﹣4x²﹣7+5x，B＝2x﹣3+3x² ，然后将两个整式关于x进行降幂排列，A＝﹣4x²+5x﹣7，B＝3x²+2x﹣3，最后只要写出其各项系数对齐同类项进行竖式计算如下：
$\begin{matrix} - 4 + 5 - 7 \\ +) 3 + 2 - 3 \\ \bar{- 1 + 7 - 10} \end{matrix}$

所以，（﹣4x²﹣7+5x）+（2x﹣3+3x²）＝﹣x²+7x﹣10

若A＝﹣4x²y²+2x³y﹣5xy³+2x⁴ ， B＝3x³y+2x²y²﹣y⁴﹣4xy³ ，请你按照小兵的方法，先对整式A，B关于某个字母进行降幂排列，再写出其各项系数进行竖式计算A﹣B，并写出A﹣B值．

查看试题解析
27. 阅读材料．
点M，N在数轴上分别表示数m和n，我们把m，n之差的绝对值叫做点M，N之间的距离，即MN=|m﹣n|．如图，在数轴上，点A，B，O，C，D的位置如图所示，则DC=|3﹣1|=|2|=2；CO=|1﹣0|=|1|=1；BC=|（﹣2）﹣1|=|﹣3|=3；AB=|（﹣4）﹣（﹣2）|=|﹣2|=2．

(1)、BD=

(2)、数轴上表示数x和数-3两点之间的距离可表示为

(3)、直接写出方程 $|x - 3| + |x + 1| = 6$ 的解是

(4)、小明发现代数式 $|x + 1| + |x - 1| + |x - 3|$ 有最小值，最小值是。此时x的值是

查看试题解析