江西省吉安市青原区2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2019-09-29 类型：期中考试

进入出卷网下载

一、单选题

1. 如果a＞b ，那么下列各式中正确的是（）

A、a﹣2＜b﹣2 B、 $\frac{a}{2} ≺ \frac{b}{2}$ C、﹣2a＜﹣2b D、﹣a＞﹣b

查看试题解析
2. 已知不等式组 ${\begin{matrix} 2 x - a < 1 \\ x - 2 b > 3 \end{matrix}$ 的解集为﹣1＜x＜1，则（a+1）（b﹣1）值为（）

A、6 B、﹣6 C、3 D、﹣3

查看试题解析
3. 如图，正方形OABC的两边OA、OC分别在x轴、y轴上，点D（5，3）在边AB上，以C为中心，把△CDB旋转90°，则旋转后点D的对应点D′的坐标是（）

A、（2，10） B、（﹣2，0） C、（2，10）或（﹣2，0） D、（10，2）或（﹣2，0）

查看试题解析
4. 小明要从甲地到乙地，两地相距1.8千米．已知他步行的平均速度为90米/分，跑步的平均速度为210米/分，若他要在不超过15分钟的时间内从甲地到达乙地，至少需要跑步多少分钟？设他需要跑步x分钟，则列出的不等式为（）

A、210x+90（15﹣x）≥1800 B、90x+210（15﹣x）≤1800 C、210x+90（15﹣x）≥1.8 D、90x+210（15﹣x）≤1.8

查看试题解析
5. △ABC中，AB=AC=5，BC=8，点P是BC边上的动点，过点P作PD⊥AB于点D，PE⊥AC于点E，则PD+PE的长是（）

A、4.8 B、4.8或3.8 C、3.8 D、5

查看试题解析
6. 如图，在直角坐标系中，已知点A（﹣3，0）、B（0，4），对△OAB连续作旋转变换，依次得到△₁、△₂、△₃、△₄、…，△₁₆的直角顶点的坐标为（）

A、（60，0） B、（72，0） C、（67 $\frac{1}{5}$ ， $\frac{9}{5}$ ） D、（79 $\frac{1}{5}$ ， $\frac{9}{5}$ ）

查看试题解析

二、填空题

7. 如图是一块长方形ABCD的场地，长AB＝a米，宽AD＝b米，从A、B两处入口的小路宽都为1米，两小路汇合处路宽为2米，其余部分种植草坪，则草坪面积为米² ．

查看试题解析
8. 如图，在平面直角坐标系xOy中，A，B两点的坐标分别为(0，2)，(-1，0)．将线段AB沿x轴的正方向平移，若点B的对应点B′坐标为(2，0)，则点A的对应点A′的坐标为．

查看试题解析
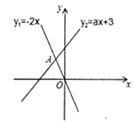
9. 如图，函数 $y_{_{1}} = - 2 x$ 与 $y_{2} = a x + 3$ 的图象相交于点A(m，2)，则关于x的不等式-2x≤ax+3的解集是.

查看试题解析
10. 若关于x的不等式组 ${\begin{matrix} x - m < 0 \\ 7 - 2 x \leq 1 \end{matrix}$ 的整数解共有4个，则m的取值范围是．

查看试题解析
11. 在RtABC中，∠C＝90°，AC＝BC＝ $\sqrt{2}$ （如图），若将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置，联结C′B ，则C′B的长为．

查看试题解析
12. 已知△ABC中，BC＝6，AB、AC的垂直平分线分别交边BC于点M、N，若MN＝2，则△AMN的周长是．

查看试题解析

三、解答题

13. 解下列不等式（组）：

(1)、 $\frac{x - 2}{2} \geq \frac{7 - x}{3}$

(2)、 ${\begin{matrix} - x + 3 < 2 x \\ \frac{x + 1}{5} - \frac{x - 2}{2} \geq 0 \end{matrix}$ ，并把它的解集表示在数轴上．

查看试题解析
14. 如图，在△ABC中，AB＝AC ， D为BC上一点，∠B＝30°，连接AD ．

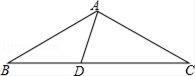(1)、若∠BAD＝45°，求证：△ACD为等腰三角形；

(2)、若△ACD为直角三角形，求∠BAD的度数．

查看试题解析
15. 如图，在平面直角坐标系中，△ABC三个顶点的坐标分别为：A（1，﹣4），B（5，﹣4），C（4，﹣1）．

(1)、将△ABC经过平移得到△A₁B₁C₁ ，若点C的应点C1的坐标为（2，5），则点A ， B的对应点A₁ ， B₁的坐标分别为；

(2)、在如图的坐标系中画出△A₁B₁C₁ ，并画出与△A₁B₁C₁关于原点O成中心对称的△A₂B₂C₂ ．

查看试题解析
16. 某市为鼓励居民节约用水，对每户用水按如下标准收费：若每户每月用水不超过8m³ ，则每m³按1元收费；若每户每月用水超过8m³ ，则超过部分每m³按2元收费．某用户7月份用水比8m³要多xm³ ，交纳水费y元．

(1)、求y关于x的函数解析式，并写出x的取值范围．

(2)、此用户要想每月水费控制在20元以内，那么每月的用水量最多不超过多少m³？

查看试题解析
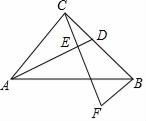
17. 已知：如图，在Rt△ABC中，∠ACB＝90°，AC＝BC ，点D是BC的中点，CE⊥AD ，垂足为点E ， BF∥AC交CE的延长线于点F ．
求证：AC＝2BF ．

查看试题解析
18. 某年级380名师生秋游，计划租用7辆客车，现有甲、乙两种型号客车，它们的载客量和租金如表．
甲种客车
乙种客车
载客量（座/辆）
60
45
租金（元/辆）
550
450

(1)、设租用甲种客车x辆，租车总费用为y元．求出y（元）与x（辆）之间的函数表达式；

(2)、当甲种客车有多少辆时，能保障所有的师生能参加秋游且租车费用最少，最少费用是多少元？

查看试题解析
19. 在△ABC中，∠B+∠ACB＝30°，AB＝4，△ABC逆时针旋转一定角度后与△ADE重合，且点C恰好成为AD中点，如图

(1)、指出旋转中心，并求出旋转角的度数．

(2)、求出∠BAE的度数和AE的长．

查看试题解析
20. 如图，在Rt△ABC中，∠ACB＝90°，点D、E分别在AB、AC上，且CE＝BC ，连接CD ，将线段CD绕点C按顺时针方向旋转90°后得到CF ，连接EF ．

(1)、求证：△BDC≌△EFC；

(2)、若EF∥CD ，求证：∠BDC＝90°．

查看试题解析
21. 如图1，已知△ABC中，AB＝AC ，点D是△ABC外一点（与点A分别在直线BC两侧），且DB＝DC ，过点D作DE∥AC ，交射线AB于E ，连接AE交BC于F ．

(1)、求证：AD垂直BC；

(2)、如图1，点E在线段AB上且不与B重合时，求证：DE＝AE；

(3)、如图2，当点E在线段AB的延长线上时，写出线段DE ， AC ， BE的数量关系．

查看试题解析
22. 为加快“秀美荆河水系生态治理工程”进度，污水处理厂决定购买10台污水处理设备．现有A ， B两种型号的设备，每台的价格分别为a万元，b万元，每月处理污水量分别为240吨，200吨．已知购买一台A型设备比购买一台B型设备多2万元，购买2台A型设备比购买3台B型设备少6万元．

(1)、求a ， b的值；

(2)、厂里预算购买污水处理设备的资金不超过105万元，你认为有哪几种购买方案；

(3)、在（2）的条件下，若每月要求处理污水量不低于2040吨，为了节约资金，请你为污水处理厂设计一种最省钱的购买方案．

查看试题解析
23. 几何探究题

(1)、发现：在平面内，若BC＝a ， AC＝b ，其中a＞b ．
当点A在线段BC上时(如图1)，线段AB的长取得最小值，最小值为；

当点A在线段BC延长线上时(如图2)，线段AB的长取得最大值，最大值为．

(2)、应用：点A为线段BC外一动点，如图3，分别以AB、AC为边，作等边△ABD和等边△ACE ，连接CD、BE ．
①证明：CD＝BE；

②若BC＝3，AC＝1，则线段CD长度的最大值为．

(3)、拓展：如图4，在平面直角坐标系中，点A的坐标为(2，0)，点B的坐标为(5，0)，点P为线AB外一动点，且PA＝2，PM＝PB ， ∠BPM＝90°．请直接写出线段AM长的最大值及此时点P的坐标．

查看试题解析

	甲种客车	乙种客车
载客量（座/辆）	60	45
租金（元/辆）	550	450