2016-2017学年四川省眉山市仁寿县龙正学区七年级下学期期中数学试卷

试卷更新日期：2017-06-28 类型：期中考试

进入出卷网下载

一、选择题

1. 下列方程中是一元一次方程的是（）

A、 $\frac{2}{x} - 1 = 0$ B、x²=1 C、2x+y=1 D、 $x - 3 = \frac{1}{2}$

查看试题解析
2. 解方程3﹣5（x+2）=x去括号正确的是（　　）

A、3﹣x+2=x B、3﹣5x﹣10=x C、3﹣5x+10=x D、3﹣x﹣2=x

查看试题解析
3. 在等式y=kx+b中，当x=2时，y=﹣4；当x=﹣2时，y=8，则这个等式是（　　）

A、y=3x+2 B、y=﹣3x+2 C、y=3x﹣2 D、y=﹣3x﹣2

查看试题解析
4. 已知 ${\begin{matrix} x = 2 \\ y = 1 \end{matrix}$ 是方程组 ${\begin{matrix} a x - 3 y = - 1 \\ x + b y = 5 \end{matrix}$ 的解，则a、b的值为（）

A、a=﹣1，b=3 B、a=1，b=3 C、a=3，b=1 D、a=3，b=﹣1

查看试题解析
5. 某商品涨价30%后欲恢复原价，则必须下降的百分数约为（　　）

A、20% B、21% C、22% D、23%

查看试题解析
6. 若方程组 ${\begin{cases} 3 x + y = 1 + 3 a \\ x + 3 y = 1 - a \end{cases}$ 的解满足x+y＞0，则a的取值范围是（）

A、a＜﹣1 B、a＜1 C、a＞﹣1 D、a＞1

查看试题解析
7. 方程2x﹣3y=7，用含x的代数式表示y为（）

A、y= $\frac{7 - 3 x}{3}$ B、y= $\frac{2 x - 7}{3}$ C、x= $\frac{7 + 3 y}{2}$ D、x= $\frac{7 - 3 y}{2}$

查看试题解析
8. 已知x+4y﹣3z=0，且4x﹣5y+2z=0，x：y：z为（　　）

A、1：2：3 B、1：3：2 C、2：1：3 D、3：1：2

查看试题解析
9. 若不等式组 ${\begin{cases} x \leq m \\ x > 3 \end{cases}$ 无解，则m的取值范围是（）

A、m＞3 B、m＜3 C、m≥3 D、m≤3

查看试题解析
10. 爷爷现在的年龄是孙子的5倍，12年后，爷爷的年龄是孙子的3倍，现在孙子的年龄是（）

A、11岁 B、12岁 C、13岁 D、14岁

查看试题解析
11. 若不等式（a+1）x＞2的解集为x＜ $\frac{2}{a + 1}$ ，则a的取值范围是（）

A、a＜1 B、a＞1 C、a＜﹣1 D、a＞﹣1

查看试题解析
12. 如图，宽为20cm的矩形图案是有10个完全一样的小长方形拼成，则其中一个小长方形的面积是（）

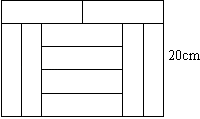A、40cm B、52cm C、64cm D、72cm

查看试题解析

二、填空题

13. 若方程（m﹣1）x²^|^m^|^﹣¹=2是一元一次方程，则m= ．

查看试题解析
14. 满足不等式﹣ $\frac{1}{2}$ x+1≥0的非负整数解是．

查看试题解析
15. 如果m，n为实数，且满足|m+n+2|+（m﹣2n+8）²=0，则mn= ．

查看试题解析
16. 当x=时，代数式 $\frac{x + 1}{2}$ 与x﹣3的值互为相反数．

查看试题解析
17. 某校春游，若包租相同的大巴13辆，那么就有14人没有座位；如果多包租1辆，那么就多了26个空位，则春游的总人数是人．

查看试题解析
18. 对于x、y定义新运算x*y=ax+by﹣3（其中a、b是常数），已知1*2=9，﹣3*3=6，则3*（﹣4）= ．

查看试题解析

三、解答题

19. 解方程或不等式（组）

(1)、 ${\begin{cases} 3 (x + y) - 4 (x - y) = 4 \\ \frac{x + y}{2} + \frac{x - y}{6} = 1 \end{cases}$

(2)、 ${\begin{cases} 2 (x + 2) \leq 3 x + 3 \\ \frac{x}{3} < \frac{x + 1}{4} \end{cases}$ （并写出不等式的整数解）

查看试题解析
20. 已知方程组 ${\begin{cases} 2 x + 5 y = - 6 \\ a x - b y = - 4 \end{cases}$ 与方程组 ${\begin{cases} 3 x - 5 y = 16 \\ b x + a y = - 8 \end{cases}$ 的解相同．求（2a+b）²⁰⁰⁴的值．

查看试题解析
21. 某商店5月1日举行促销优惠活动，当天到该商店购买商品有两种方案，方案一：用168元购买会员卡成为会员后，凭会员卡购买商店内任何商品，一律按商品价格的8折优惠；方案二：若不购买会员卡，则购买商店内任何商品，一律按商品价格的9.5折优惠．已知小敏5月1日前不是该商店的会员．

(1)、若小敏不购买会员卡，所购买商品的价格为120元时，实际应支付多少元？

(2)、请帮小敏算一算，所购买商品的价格在什么范围时，采用方案一更合算？

查看试题解析
22. 抗洪指挥部的一位驾驶员接到一个防洪的紧急任务，要在限定的时内把一批抗洪物质从物质局运到水库，这辆车如果按每小时30千米的速度行驶在限定的时间内赶到水库，还差3千米，他决定以每小时40千米的速度前进，结果比限定时间早到18分钟，问限定时间是几小时？物质局仓库离水库有多远？

查看试题解析
23. 已知二元一次方程组 ${\begin{cases} 3 x + 4 y = 2 k - 3 \\ 2 x - y = 3 k + 4 \end{cases}$ 的解的和是2，求x、y、k的值．

查看试题解析
24. 销售有限公司到某汽车制造有限公司选购A、B两种型号的轿车，用300万元可购进A型轿车10辆，B型轿车15辆；用300万元可购进A型轿车8辆，B型轿车18辆．

(1)、求A、B两种型号的轿车每辆分别多少元？

(2)、若该汽车销售公司销售一辆A型轿车可获利8000元，销售一辆B型轿车可获利5000元，该汽车销售公司准备用不超过400万元购进A、B两种型号轿车共30辆，且这两种轿车全部售出后总获利不低于20.4万元，问：有几种购车方案？在这几种购车方案中，哪种获利最多？

查看试题解析
25. 阅读下列材料，然后解答后面的问题．
我们知道方程2x+3y=12有无数组解，但在实际生活中我们往往只需要求出其正整数解．例：由2x+3y=12，得 $y = \frac{12 - 2 x}{3} = 4 - \frac{2}{3} x$ ，（x、y为正整数）∴ ${\begin{cases} x > 0 \\ 12 - 2 x > 0 \end{cases}$ 则有0＜x＜6．又 $y = 4 - \frac{2}{3} x$ 为正整数，则 $\frac{2}{3} x$ 为正整数．
由2与3互质，可知：x为3的倍数，从而x=3，代入 $y = 4 - \frac{2}{3} x = 2$ ．
∴2x+3y=12的正整数解为 ${\begin{cases} x = 3 \\ y = 2 \end{cases}$
问题：

(1)、请你写出方程2x+y=5的一组正整数解：

(2)、若 $\frac{6}{x - 2}$ 为自然数，则满足条件的x值有个；

A、2 B、3 C、4 D、5

(3)、七年级某班为了奖励学习进步的学生，购买了单价为3元的笔记本与单价为5元的钢笔两种奖品，共花费35元，问有几种购买方案？

查看试题解析