初中数学华师大版九年级上学期 第22章测试卷

试卷更新日期：2019-09-27 类型：单元试卷

进入 出卷网 下载

一、单选题

  • 1. 已知关于x的一元二次方程 (a−1)x2−2x+a2−1=0 有一个根为 x=0 ，则a的值为（    ）
    A、0 B、±1 C、1 D、−1

    查看试题解析

  • 2. 用配方法解方程x2-3x-3=0时，配方结果正确的是（ ）
    A、(x-3)2=3 B、(x- 32 )2=3 C、(x-3)2= 34 D、(x- 32 )2= 214

    查看试题解析

  • 3. 关于x的一元二次方程x2-4x+m＝0的两实数根分别为x1、x2 ， 且x1+3x2＝5，则m的值为（   ）
    A、74 B、75 C、76 D、0

    查看试题解析

  • 4. 用配方法解方程 x2+8x+9=0 ，变形后的结果正确的是（ ）
    A、(x+4)2=−9 B、(x+4)2=−7 C、(x+4)2=25 D、(x+4)2=7

    查看试题解析

  • 5. 若关于x的一元二次方程 x2+2x−k=0 有两个不相等的实数根，则k的取值范围是（    ）
    A、k<−1 B、k>−1 C、k<1 D、k>1

    查看试题解析

二、填空题

  • 6. 已知关于 x 的方程 ax2+2x−3=0 有两个不相等的实数根，则 a 的取值范围是 ．

    查看试题解析

  • 7. 若关于x的一元二次方程x2+mx+2m-4=0有一个根为x=-1，则m= 。

    查看试题解析

  • 8. 已知一个一元二次方程的二次项系数是2，常数项是－14，它的一个根是－7，则这个方程为 ．

    查看试题解析

三、计算题

  • 9. 解方程：
    (1)、9x2=(x−1)2
    (2)、34x2−2x−12=0

    查看试题解析

  • 10.      
    (1)、计算: (−3)2−(2−3)(2+3)−8
    (2)、解方程:x2+6x+8=0

    查看试题解析

  • 11. 先化简，再求值： (1+5x−2)÷x2−9x−3 ，其中 x 是方程 x2−4x+1=0 的实数根.

    查看试题解析

四、综合题

  • 12. 已知关于x的方程kx2-3x+1=0有实数根
    (1)、求k的取值范围
    (2)、若该方程有两个实数根,分别为x1和x2,当x1+x2+x1x2=4时,求k的值

    查看试题解析

  • 13. 已知m，n是实数，定义运算“*”为：m*n＝mn+n．
    (1)、分别求4*（﹣2）与4* 5 的值；
    (2)、若关于x的方程x*（a*x）＝﹣ 14 有两个相等的实数根，求实数a的值．

    查看试题解析

  • 14. 如图，直线MN与x轴，y轴分别相交于A，C两点，分别过A，C两点作x轴y轴的垂线相交于B点，且OA，OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根．

    (1)、求C点坐标；
    (2)、求直线MN的解析式；
    (3)、在直线MN上存在点P，使以P，B，C三点为顶点的三角形是等腰三角形．请直接写出P点坐标．

    查看试题解析

  • 15. 林场要建一个果园(如图矩形ABCD)，果园的一向靠墙(墙最大可用长度为25米)，另三边用木栏围成，在BC上开一个宽为1米的门(不用木栏)，小栏总长63米，计划建果园面积为440平方米．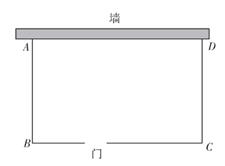

    (1)、求AB的长；
    (2)、  现在准备在地面上为种植果树打一些面积固定的框，要求每个框的面积a不少于0.4平方米，但又不超过0.44平方米，请写出果园内打框的个数y关于a的解析式，并求出y的取值范围．

    查看试题解析

  • 16. 习近平总书记说：“读书可以让人保持思想活力，让人得到智慧启发，让人滋养浩然之气”．某校为响应我市全民阅读活动，利用节假日面向社会开放学校图书馆．据统计，第一个月进馆 128 人次，进馆人次逐月增加，到第三个月末累计进馆 608 人次，若进馆人次的月平均增长率相同．
    (1)、求进馆人次的月平均增长率；
    (2)、因条件限制，学校图书馆每月接纳能力不超过 500 人次，在进馆人次的月平均增长率不变的条件下，校图书馆能否接纳第四个月的进馆人次，并说明理由．

    查看试题解析