四川省成都市金堂县2018-2019学年八年级上学期数学期中考试试卷

试卷更新日期：2019-09-26 类型：期中考试

进入出卷网下载

一、单选题

1. 下列实数中，是有理数的为（）

A、 $\sqrt{2}$ B、 $\sqrt[3]{4}$ C、π D、0

查看试题解析
2. 若 $5 + \sqrt{11}$ 与 $5 - \sqrt{11}$ 的整数部分分别为 $x ， y$ ，则 $x + y$ 的立方根是（）

A、 $\sqrt[3]{9}$ B、 $\pm \sqrt[3]{3}$ C、3 D、 $\pm \sqrt[3]{9}$

查看试题解析
3. 若式子 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围是（）

A、x＜2 B、x＞2 C、x≤2 D、x≥2

查看试题解析
4. 下列一组数是勾股数的是（）

A、6，7，8 B、5，12，13 C、0.3，0.4，0.5 D、10，15，18

查看试题解析
5. 象棋在中国有着三千多年的历史，由于用具简单，趣味性强，成为流行极为广泛的益智游戏．如图，是一局象棋残局，已知表示棋子“馬”和“車”的点的坐标分别为(4，3)，(－2，1)，则表示棋子“炮”的点的坐标为（）

A、(－3，3) B、(3，2) C、(0，3) D、(1，3)

查看试题解析
6. 根据下列表述，能确定位置的是（）

A、国际影城3排 B、A市南京路口 C、北偏东60° D、东经100°，北纬30°

查看试题解析
7. 一次函数 $y = k x + b$ 的图象如图所示，则关于x的方程 $k x + b = - 1$ 的解为 $($ $)$

A、 $x = 0$ B、 $x = 1$ C、 $x = \frac{1}{2}$ D、 $x = - 2$

查看试题解析
8. 已知，如图长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为（）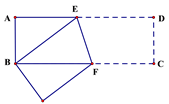

A、3cm² B、4cm² C、6cm² D、12cm²

查看试题解析
9. 点M(3，-4)关于y的轴的对称点是M₁ ，则M₁关于x轴的对称点M₂的坐标为（）

A、（-3，4） B、（-3，-4） C、(3，4) D、（3，-4）

查看试题解析
10. 函数y=kx﹣k（k＜0）的大致图象是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. $\sqrt[3]{8}$ 的平方根是．

查看试题解析
12. 计算： $\sqrt{3}$ （ $\sqrt{3}$ + $\sqrt{27}$ ）= ．

查看试题解析
13. 如图，将一根25㎝长的细木棒放入长、宽、高分别为8㎝、6㎝和10 $\sqrt{3}$ ㎝的长方体无盖盒子中，则细木棒露在盒外面的最短长度是㎝．

查看试题解析
14. 若函数y＝（a+3）x+a²﹣9是正比例函数，则a＝．

查看试题解析
15. 已知a、b、c位置如图所示，试化简：|a+b﹣c|+ $\sqrt{{(b - a)}^{2}}$ = ．

查看试题解析
16. 若 $\sqrt{x - 3}$ +（y+1）⁴=0，则x^y= ．

查看试题解析
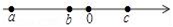17. 已知直线a平行于y轴，且直线a上任意一点的横坐标都是3，直线b平行于x轴，且直线b与x轴的距离为2，直线a与b交点为P，则点P的坐标为．

查看试题解析
18. 如图，四边形ABCD的对角线AC与BD互相垂直，若AB＝3，BC＝4，CD＝5，则AD的长为．

查看试题解析
19. 如图，OP=1，过P作PP₁⊥OP ，得OP₁= $\sqrt{2}$ ；再过P₁作P₁P₂⊥OP₁且P₁P₂=1，得OP₂= $\sqrt{3}$ ；又过P₂作P₂P₃⊥OP₂且P₂P₃=1，得OP₃=2；…依此法继续作下去，得OP₂₀₁₉= ．

查看试题解析

三、解答题

20.

(1)、计算： $\sqrt{16}$ +（2﹣ $\sqrt{2}$ ）⁰﹣（﹣ $\frac{1}{2}$ ）^﹣²+|﹣1|

(2)、计算：2 $\sqrt{12}$ •（3 $\sqrt{48}$ ﹣4 $\sqrt{\frac{1}{8}}$ ﹣3 $\sqrt{27}$ ）

查看试题解析
21. 已知：2m＋2的平方根是±4；3m＋n的立方根是－1，求：2m－n的算术平方根．

查看试题解析
22. 一架云梯长25 m，如图所示斜靠在一面墙上，梯子底端C离墙7 m.

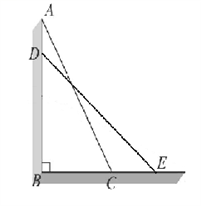(1)、这个梯子的顶端A距地面有多高？

(2)、如果梯子的顶端下滑了4 m，那么梯子的底部在水平方向也是滑动了4 m吗？

查看试题解析
23. 如图

(1)、如图所示，∠B=∠OAF=90°，BO=3cm ， AB=4cm ， AF=12cm ，求图中半圆的面积．

(2)、在直角坐标系内，一次函数y=kx+b的图象经过三点A（2，0），B（0，2），C（m ， 3）．求这个一次函数解析式并求m的值．

查看试题解析
24. 如图，△ABC在平面直角坐标系中：

(1)、画出△ABC关于y轴对称的△DEF（其中D、E、F是A、B、C的对应点）

(2)、写出D、E、F的坐标；

(3)、求出△DEF的面积．

查看试题解析
25. 某移动公司有两类收费标准：A类收费是不管通话时间多长，每部手机每月须缴月租12元．另外，通话费按0.2元/min；B类收费是没有月租，但通话费按0.25元/min ．

(1)、请分别写出每月应缴费用y（元）与通话时间x（min）之间的关系式；

(2)、若小芳爸爸每月通话时间为300min ，请说明选择哪种收费方式更合算；

(3)、每月通话多长时间，按A、B两类收费标准缴费，所缴话费相等．

查看试题解析
26. 某超市预购进A、B两种品牌的T恤共200件，已知两种T恤的进价如表所示，设购进A种T恤x件，且所购进的两种T恤全部卖出，获得的总利润为W元．

(1)、求W关于x的函数关系式；

(2)、如果购进两种T恤的总费用为9500元，求超市所获利润．（提示：利润=售价﹣进价）

品牌

进价（元/件）

售价（元/件）

A

50

80

B

40

65

查看试题解析
27. 小明在解决问题：已知a= $\frac{1}{2 + \sqrt{3}}$ ，求2a²﹣8a+1的值，他是这样分析与解的：
∵a= $\frac{1}{2 + \sqrt{3}}$ = $\frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3}}$ =2﹣ $\sqrt{3}$

∴a﹣2=﹣ $\sqrt{3}$

∴（a﹣2）²=3，a²﹣4a+4=3

∴a²﹣4a=﹣1

∴2a²﹣8a+1=2（a²﹣4a）+1=2×（﹣1）+1=﹣1

请你根据小明的分析过程，解决如下问题：

(1)、化简 $\frac{1}{\sqrt{2} + 1}$ + $\frac{1}{\sqrt{3} + \sqrt{2}}$ + $\frac{1}{\sqrt{4} + \sqrt{3}}$ +…+ $\frac{1}{\sqrt{100} + \sqrt{99}}$

(2)、若a= $\frac{1}{\sqrt{2} - 1}$ ，求4a²﹣8a+1的值．

查看试题解析
28. 如图，直线l₁：y=﹣x+3与x轴相交于点A，直线l₂：y=kx+b经过点（3，﹣1），与x轴交于点B（6，0），与y轴交于点C，与直线l₁相交于点D．

(1)、求直线l₂的函数关系式；

(2)、点P是l₂上的一点，若△ABP的面积等于△ABD的面积的2倍，求点P的坐标；

(3)、设点Q的坐标为（m，3），是否存在m的值使得QA+QB最小？若存在，请求出点Q的坐标；若不存在，请说明理由．

查看试题解析

品牌	进价（元/件）	售价（元/件）
A	50	80
B	40	65