湖南省张家界市慈利县2018-2019学年八年级上学期数学期中考试试卷

试卷更新日期：2019-09-26 类型：期中考试

进入出卷网下载

一、单选题

1. 分式 $\frac{x^{2} - 4}{x + 2}$ 的值为0，则（）

A、x=2 B、x=﹣2 C、x=±2 D、x=0

查看试题解析
2. 下列等式或不等式成立的是（）

A、 $3^{2} < 2^{3}$ B、 ${(- 3)}^{- 2} < {(- 2)}^{- 3}$ C、 $9 \times 10^{3} \div 3 \times 10^{4} = 30$ D、 ${(- 0.1)}^{- 2} > 1$

查看试题解析
3. 若 $x y = x - y \neq 0$ ，则分式 $\frac{1}{x} - \frac{1}{y}$ 等于（）

A、 $\frac{1}{x y}$ B、 $y - x$ C、1 D、 $- 1$

查看试题解析
4. 分式 $\frac{1}{2 x} ， \frac{1}{2 y^{2}} ， - \frac{1}{5 x y}$ 的最简公分母为（）

A、2xy² B、5xy C、10xy² D、10x²y²

查看试题解析
5. 以下列各组线段为边，能组成三角形的是（）

A、1cm，2cm，3cm B、4cm，6cm，8cm， C、5cm，6cm，12cm， D、2cm，3cm，5cm

查看试题解析
6. 下列命题的逆命题一定成立的是（）
①对顶角相等； ②同位角相等，两直线平行；③全等三角形的周长相等；④面积相等的两个三角形全等

A、①②③ B、①④ C、②④ D、②

查看试题解析
7. 小明用一根长20cm的铁丝做一个周长是20cm的等腰三角形，则腰长x的取值范围是（）

A、0＜x＜10 B、0＜x＜5 C、5≤x≤10 D、5＜x＜10

查看试题解析
8. 如图所示，在△ABC中，∠BAC=106°，EF、MN分别是AB、AC的垂直平分线，E、M在BC上，则∠EAM等于（）

A、58° B、32° C、36° D、34°

查看试题解析

二、填空题

9. 化简： $\frac{x - y}{y^{2} - x^{2}}$ =.

查看试题解析
10. 红细胞的平均直径为 $0.0000077 m$ ，将0.0000077用科学记数法表示为．

查看试题解析
11. 若2018^m＝6，2018ⁿ＝4，则2018^2m^﹣ⁿ＝．

查看试题解析
12. 如图，在△ABC中，∠B与∠C的角平分线交于点O. 过O点作DE∥BC ，分别交AB、AC于D．E.若AB=8，AC=6，则△ADE的周长是.

查看试题解析
13. 等腰三角形的一个角为40°，则它的底角为.

查看试题解析
14. 已知线段a ， b ， c ，求作△ABC ，使BC=a ， AC=b ， AB=c ，下面作法的合理顺序为 (填序号)①分别以B ， C为圆心，c ， b为半径作弧，两弧交于点A；②作直线BP ，在BP上截取BC=a；③连接AB ， AC ， △ABC为所求作的三角形。

查看试题解析

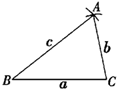
三、解答题

15. 计算： ${(- x^{3} y^{- 2})}^{- 2} \div x^{- 6} {(π - 2018)}^{0}$

查看试题解析
16. 解方程: $\frac{x}{x- 2} - \frac{2}{x^{2} - 4}$ =1.

查看试题解析
17. 先化简 $\frac{x - 4}{x^{2} - 9} \div (\frac{1}{x - 3} - 1)$ 再从 $\frac{1}{3}$ 、3、4中选一个你喜欢的数代入求值.

查看试题解析
18. 列方程或方程组解应用题：
小马自驾私家车从A地到B地，驾驶原来的燃油汽车所需油费108元，驾驶新购买的纯电动车所需电费27元，已知每行驶1千米，原来的燃油汽车所需的油费比新购买的纯电动汽车所需的电费多0.54元，求新购买的纯电动汽车每行驶1千米所需的电费．

查看试题解析
19. 如图，AD⊥BD，AE平分∠BAC，∠B=30°，∠ACD=70°．求∠AED的度数．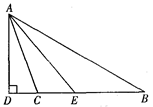

查看试题解析
20. 如图，点B，F，C，E在直线l上（F，C之间不能直接测量），点A，D在l异侧，测得AB=DE，AC=DF，BF=EC.

(1)、求证：△ABC≌△DEF；

(2)、指出图中所有平行的线段，并说明理由.

查看试题解析
21. 在等边三角形ABC中，点P在△ABC内，点Q在△ABC外，且∠ABP=∠ACQ，BP=CQ.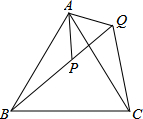

(1)、求证：△ABP≌△CAQ；

(2)、请判断△APQ是什么形状的三角形？试说明你的结论.

查看试题解析
22. 如图，AB∥CD，以点A为圆心，小于AC长为半径作圆弧，分别交AB，AC于E，F两点，再分别以E，F为圆心，大于 $\frac{1}{2}$ EF长为半径作圆弧，两条圆弧交于点P，作射线AP，交CD于点M。

(1)、若∠ACD=114°，求∠MAB的度数；

(2)、若CN⊥AM，垂足为N，求证：△ACN≌△MCN。

查看试题解析
23. 如图，已知正方形ABCD的边长为10厘米，点E在边AB上，且AE=4厘米，如果点P在线段BC上以2厘米/秒的速度由B点向C点运动，同时，点Q在线段CD上由C点向D点运动．设运动时间为t秒．

(1)、若点Q的运动速度与点P的运动速度相等，经过2秒后，△BPE与△CQP是否全等？请说明理由；

(2)、若点Q的运动速度与点P的运动速度不相等，则当t为何值时，能够使△BPE与△CQP全等；此时点Q的运动速度为多少．

查看试题解析