四川省巴中市恩阳区2017-2018学年九年级上学期数学期中考试试卷
试卷更新日期:2019-09-26 类型:期中考试
一、单选题
-
1. 下列二次根式中,与 是同类二次根式的是( )A、 B、 C、 D、2. 若方程(m-1)x2+ x-2=0是关于x的一元二次方程,则m的取值范围是( )。A、m = 0 B、m ≠ 1 C、m ≥0且m ≠ 1 D、m 为任意实数3. 三角形两边的长分别是8和6,第三边的长是一元二次方程x2﹣16x+60=0的一个实数根,则该三角形的面积是( )
A、24 B、24或8 C、48 D、84. 下列计算中,正确的是( )A、 B、 C、 D、5. 化简 的结果为 ( )A、 B、- C、- D、6. 如图,F是平行四边形ABCD对角线BD上的点,BF∶FD=1∶3,则BE∶EC=( ) A、 B、 C、 D、7. “学在恩阳、生态教育”恩阳区自成区以来一直把教育放在优先发展的地位,教育教学质量得到了空前的提升,特别是近两年高考更是捷报频频,得到了社会各界和老百姓的好评。2015年高考重本上线50人,到2017年重本上线218人,设每年增长的百分率为 ,则列出方程正确的是( )A、 B、 C、 D、8. 关于x的方程ax2+bx+c=0,若满足a-b+c=0。则方程( ).A、必有一根为1 B、必有两相等实根 C、必有一根为-1 D、没有实数根。9. 下列四个三角形,与左图中的三角形相似的是( )
A、 B、 C、 D、7. “学在恩阳、生态教育”恩阳区自成区以来一直把教育放在优先发展的地位,教育教学质量得到了空前的提升,特别是近两年高考更是捷报频频,得到了社会各界和老百姓的好评。2015年高考重本上线50人,到2017年重本上线218人,设每年增长的百分率为 ,则列出方程正确的是( )A、 B、 C、 D、8. 关于x的方程ax2+bx+c=0,若满足a-b+c=0。则方程( ).A、必有一根为1 B、必有两相等实根 C、必有一根为-1 D、没有实数根。9. 下列四个三角形,与左图中的三角形相似的是( )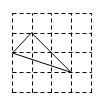 A、
A、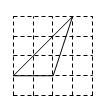 B、
B、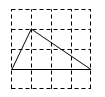 C、
C、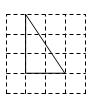 D、
D、 10. 如图,已知AD是△ABC的中线,AE=EF=FC,下面给出三个关系式:①AG:AD=1:2;②GE:BE=1:3③BE:BG=4:3,其中正确的是( )
10. 如图,已知AD是△ABC的中线,AE=EF=FC,下面给出三个关系式:①AG:AD=1:2;②GE:BE=1:3③BE:BG=4:3,其中正确的是( ) A、①②③ B、①② C、②③ D、①③
A、①②③ B、①② C、②③ D、①③二、填空题
-
11. 化简: , =.12. 当x 时,二次根式 有意义。13. 已知(x2+y2+1)2=81,则x2+y2=14. 若实数a、b满足a2-7a+2=0和b2-7b+2=0,则式子 的值是.15. 若实数a、b满足|a+2|+ =0,则 = .16. 最简二次根式 与 的被开方数相同,则 的值为.17. 若 = = =0.5,则 =.18. 如果一个三角形的三边长为5、12、13,与其相似的三角形的最长边的长为52,那么此三角形的周长为 , 面积为 .19. 如图,正方形ABCD中,点N为AB的中点,连接DN并延长交CB的延长线于点P , 连接AC交DN于点M , 若PN=3,则DM的长为 .
 20. 如图,△ABC中,∠C=90°,AC=BC=2,取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1 , 作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1 , 它的面积记作S2 . 照此规律作下去,则S2017=.
20. 如图,△ABC中,∠C=90°,AC=BC=2,取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1 , 作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1 , 它的面积记作S2 . 照此规律作下去,则S2017=.
三、解答题
-
21. 计算:(1)、(2)、22. 解方程:(1)、(x-2)2=16(2)、2x(x-3)=x-3.(3)、3x2-9x+6=0(4)、5x2+2x-3=0(用求根公式)23. 先化简,在求值: ,其中a= .24. 已知 是方程组 的一组解,求此方程组的另一组解.25. 已知:关于x的方程x2-(m-1)x-2m2+m=0(1)、求证:无论m为何实数,方程总有实数根;(2)、若此方程有两个实数根x1 , x2 , 且 x12+x22=2 ,求m的值.26. 阅读下列材料,然后回答问题:
在进行二次根式运算时,我们有时会碰上如 、 这样的式子,其实我们还可以将其进一步化简: ;
.
以上这种化简过程叫做分母有理化.
还可以用以下方法化简:
= = = = ﹣1.
请任用其中一种方法化简:
① ;② ;
27. 春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准:
某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
28. 如图,△ABC中,AD是∠BAC的平分线,AD的垂直平分线交AD于点E,交BC的延长线于点F.求证:△ABF∽△CAF. 29. 如图,在平面直角坐标系中,已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上,并且OA、OB的长分别是方程x2-7x+12=0的两根(OA<OB),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒.
29. 如图,在平面直角坐标系中,已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上,并且OA、OB的长分别是方程x2-7x+12=0的两根(OA<OB),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒. (1)、求A、B两点的坐标.(2)、求当t为何值时,△APQ与△AOB相似?30. 正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,
(1)、求A、B两点的坐标.(2)、求当t为何值时,△APQ与△AOB相似?30. 正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,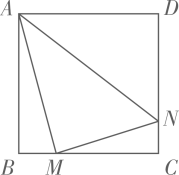 (1)、证明:Rt△ABM ∽Rt△MCN;(2)、设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式;当M点运动到什么位置时,四边形ABCN的面积最大,并求出最大面积;(3)、当M点运动到什么位置时Rt△ABM∽Rt△AMN,求此时x的值.
(1)、证明:Rt△ABM ∽Rt△MCN;(2)、设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式;当M点运动到什么位置时,四边形ABCN的面积最大,并求出最大面积;(3)、当M点运动到什么位置时Rt△ABM∽Rt△AMN,求此时x的值.