湖南省张家界市永定区2018-2019学年九年级上学期数学期中考试试卷

试卷更新日期：2019-09-26 类型：期中考试

进入出卷网下载

一、单选题

1. 已知点P(－l，4)在反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象上，则k的值是（）

A、 $- \frac{1}{4}$ B、 $\frac{1}{4}$ C、4 D、－4

查看试题解析
2. 已知蓄电池的电压为定值，使用蓄电池时，电流I(单位：A)与电阻R(单位：Ω)是反比例函数关系，它的图象如图所示．则用电阻R表示电流I的函数表达式为（）

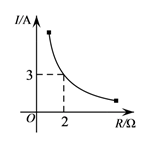A、 $I = \frac{3}{R}$ B、 $I = - \frac{6}{R}$ C、 $I = - \frac{3}{R}$ D、 $I = \frac{6}{R}$

查看试题解析
3. 用配方法解一元二次方程x²+4x﹣1=0，此方程可变形为（）

A、（x+2）²=5 B、（x﹣2）²= 5 C、（x+2）²=1 D、（x﹣2）²=1

查看试题解析
4. 已知点A（1，y₁），B（2，y₂），C（﹣2，y₃），都在反比例y= $\frac{- 2}{x}$ 的图象上，则（）

A、y₁＞y₂＞y₃ B、y₃＞y₂＞y₁ C、y₂＞y₃＞y₁ D、y₁＞y₃＞y₂

查看试题解析
5. 若关于x的一元二次方程（k﹣1）x²+6 x +3=0有实数根，则实数k的取值范围为（）

A、k＜4 B、k＜4，且k≠1 C、k≤4 D、k≤4，且k≠1

查看试题解析
6. 如图，在 $△ A B C$ 中， $D E ∥ B C$ ，分别交 $A B$ ， $A C$ 于点 $D$ ， $E$ ．若 $A E = 3$ ， $E C = 6$ ，则 $\frac{D E}{B C}$ 的值为（）

A、 $\frac{1}{9}$ B、 $\frac{1}{6}$ C、 $\frac{1}{4}$ D、 $\frac{1}{3}$

查看试题解析
7. 如图， $A C$ 与 $B D$ 相交于点 $E$ ， $A D / / B C$ ．若 $A E ： E C = 1 ： 2$ ，则 $S_{△ A E D} ： S_{△ C E B}$ 为（）

A、 $1 ： \sqrt{2}$ B、 $1 ： 2$ C、 $1 ： 3$ D、 $1 ： 4$

查看试题解析
8. 某市2015年底已有绿化面积300公顷，经过两年绿化，绿化面积逐年增加，到2017年底增加到363公顷．设绿化面积平均每年的增长率为x ，由题意，所列方程正确的是（）

A、300（1+ x）=363 B、300（1+2 x）=363 C、300（1+ x）²=363 D、363（1﹣x）²=300

查看试题解析

二、填空题

9. 已知反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象在其每一分支上， $y$ 随 $x$ 的增大而增大，则此反比例函数的解析式可以是．（注：只需写出一个正确答案即可）

查看试题解析
10. 若一元二次方程（m+2）x²+m²﹣4=0的常数项为0，则m= ．

查看试题解析
11. 若m是方程2x²﹣3x﹣1=0的一个根，则6m²﹣9m+2018的值为．

查看试题解析
12. 如图， $△ A B C$ 和 $△ A_{1} B_{1} C_{1}$ 是以点 $O$ 为位似中心的位似三角形，若 $C_{1}$ 为 $O C$ 的中点， $A_{1} B_{1}$ =4，则AB的长为．

查看试题解析
13. 若 $\frac{x - 2 y}{y} = \frac{3}{4}$ ，则 $\frac{x}{y}$ = ．

查看试题解析
14. 如图，在直角坐标系中，正方形的中心在原点O，且正方形的一组对边与x轴平行，点P（3a，a）是反比例函数 $y = \frac{k}{x}$ （k＞0）的图象上与正方形的一个交点．若图中阴影部分的面积等于9，则这个反比例函数的解析式为．

查看试题解析

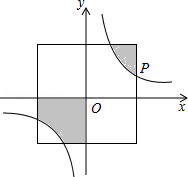
三、解答题

15. 解下列方程：

(1)、 $x^{2} - 3 x = 0$

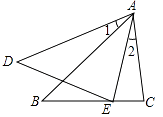
(2)、 $5 x^{2} - 4 x - 1 = 0$ .

查看试题解析
16. 已知关于x的方程x²+mx+m-2=0.

(1)、若此方程的一个根为1,求m的值；

(2)、求证：不论m取何实数,此方程都有两个不相等的实数根.

查看试题解析
17. 如图，已知∠1=∠2，∠AED=∠C，求证：△ABC∽△ADE

查看试题解析
18. 如图，在平面直角坐标系中，每个小正方形的边长为1，△ABC各顶点都在格点上，结合所给的平面直角坐标系解答下列问题：

(1)、以O为位似中心作一个与△ABC位似的△A₁B₁C₁ ，使△A₁B₁C₁与△ABC的位似比为2；

(2)、直接写出点A₁、B₁、C₁的坐标．

查看试题解析
19. 如图所示，在△ABC中，∠B=90°，BC=8cm，AB=6cm．点P从点A开始沿AB边向点B以1cm ∕s的速度移动，点Q从点B开始沿BC边向点C以4 cm ∕ s的速度移动．如果点P、Q分别从点A、B同时出发，经过几秒钟，△PBQ的面积等于10cm²？

查看试题解析
20. 已知一次函数y＝kx＋b和反比例函数y＝ $\frac{m}{x}$ 图象相交于A(-4，2)，B(n ，－4)两点.

(1)、求一次函数和反比例函数的解析式；

(2)、求△AOB的面积；

(3)、观察图象，直接写出不等式kx＋b－ $\frac{m}{x}$ ＜0的解集．

查看试题解析
21. 如图，小明在地面上放置一个平面镜 $E$ 来测量铁塔 $A B$ 的高度，镜子与铁塔的距离 $E B = 20$ 米，镜子与小明的距离 $E D = 2$ 米时，小明刚好从镜子中看到铁塔顶端 $A$ ．已知小华的眼睛距地面的高度CD=1.6米，求铁塔 $A B$ 的高度．（根据光的反射原理， $∠ 1 = ∠ 2$ ）

查看试题解析
22. 如图， $Δ A B C$ 的内角平分线 $A P$ 与外角平分线 $A Q$ 分别交 $B C$ 及 $B C$ 的延长线于点 $P$ ， $Q$ .

(1)、求 $∠ P A Q$ 的度数；

(2)、若点 $M$ 为 $P Q$ 的中点，求证： $P M^{2} = C M • B M$ ．

查看试题解析