湖南省汨罗市弼时片区2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期:2019-09-26 类型:期中考试
一、单选题
-
1. 已知点M (-2,3 )在双曲线上,则下列一定在该双曲线上的是( )A、(3,-2 ) B、(-2,-3 ) C、(2,3 ) D、(3,2)2. 已知:如图,在△ABC中,∠ADE=∠C,则下列等式成立的是 ( )
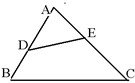 A、 B、 C、 D、3. 如图,在函数 的图象上取三点A、B、C,由这三点分 别向x轴、y轴作垂线,设矩形AA1OA2、BB1OB2、CC1OC2 的 面积分别为SA、SB、SC , 则下列正确的是( )
A、 B、 C、 D、3. 如图,在函数 的图象上取三点A、B、C,由这三点分 别向x轴、y轴作垂线,设矩形AA1OA2、BB1OB2、CC1OC2 的 面积分别为SA、SB、SC , 则下列正确的是( ) A、SA<SB<SC B、SA>SB>SC C、SA=SC=SB D、SA<SC<SB4. 反比例函数y= 和一次函数y=kx-k在同一坐标系中的图象大致是( )A、
A、SA<SB<SC B、SA>SB>SC C、SA=SC=SB D、SA<SC<SB4. 反比例函数y= 和一次函数y=kx-k在同一坐标系中的图象大致是( )A、 B、
B、 C、
C、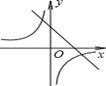 D、
D、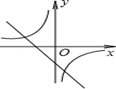 5. 一元二次方程 ,用配方法解该方程,配方后的方程为( )A、 B、 C、 D、6. 方程 是关于 的一元二次方程,则( )A、 B、 C、 D、7. 如图,D、E是AB的三等分点,DF∥EG∥BC,图中三部分的面积分别为S1 , S2 , S3 , 则S1:S2:S3=( )
5. 一元二次方程 ,用配方法解该方程,配方后的方程为( )A、 B、 C、 D、6. 方程 是关于 的一元二次方程,则( )A、 B、 C、 D、7. 如图,D、E是AB的三等分点,DF∥EG∥BC,图中三部分的面积分别为S1 , S2 , S3 , 则S1:S2:S3=( )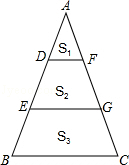 A、1:2:3 B、1:2:4 C、1:3:5 D、2:3:48. 某钢铁厂今年1月份钢产量为5000吨,3月份上升到7200吨,设平均每月增长的百分率为 ,根据题意得方程( )A、5000(1+x)+5000(1+x)2=7200 B、5000(1+x2)=7200 C、5000(1+x)2=7200 D、5000+5000(1+x)2=7200
A、1:2:3 B、1:2:4 C、1:3:5 D、2:3:48. 某钢铁厂今年1月份钢产量为5000吨,3月份上升到7200吨,设平均每月增长的百分率为 ,根据题意得方程( )A、5000(1+x)+5000(1+x)2=7200 B、5000(1+x2)=7200 C、5000(1+x)2=7200 D、5000+5000(1+x)2=7200二、填空题
-
9. 已知关于x的一元一次方程x2+3x+1-m=0 ,请你自选一个m的值,使方程没有实数根m=.10. 已知x1 , x2是方程x2﹣3x+1=0的两个实数根,则 = .11. 如果反比例函数 的图象经过点(3,1),那么k=。12. 在反比例函数 的图象上的图象在二、四象限,则 的取值范围是.13. 一个4米高的电线杆的影长是6米,它临近的一个建筑物的影长是36米.则这个建筑的高度是m.14. 电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体,若舞台
AB长为20m,试问主持人应走到离A点至少m处?
15. 如图,若DE∥BC,FD∥AB,AD∶AC=2∶3 ,AB=9,BC=6,则四边形BEDF的周长为. 16. 已知等腰三角形的一边为3,另两边是方程 的两个实根,则m的值为.
16. 已知等腰三角形的一边为3,另两边是方程 的两个实根,则m的值为.三、解答题
-
17. 解下列方程:(1)、x2-5x+6=0(2)、2x2+5x+2=018. 已知:3是方程x2-2x+c=0的一个根,求方程的另一个根及c的值.19. 已知:关于x的一元二次方程: kx2+2(k+1)x+k=0有两个实数根,求k的取值范围.20. 已知正比例函数y=kx与比例函数 的图象都过点A(m,1).求:(1)、正比例函数的表达式;(2)、正比例函数图象与反比例数图象的另一个交点的坐标.21. 如图,在△ABC中,DE∥BC,EF∥AB.
 (1)、求证:△ADE∽△EFC;(2)、如果AB=6,AD=4,求 的值.22. 如图,Rt△ABO的顶点A是双曲线 与直线 在第二象限的交点,AB⊥ 轴于B且S△ABO= .
(1)、求证:△ADE∽△EFC;(2)、如果AB=6,AD=4,求 的值.22. 如图,Rt△ABO的顶点A是双曲线 与直线 在第二象限的交点,AB⊥ 轴于B且S△ABO= . (1)、求这两个函数的解析式;(2)、求直线与双曲线的两个交点A,C的坐标和△AOC的面积。23. 如图,某农场要建一个长方形的养鸡场,鸡场的一边靠墙,墙长25m,另外三边用木栏围着,木栏长40m.
(1)、求这两个函数的解析式;(2)、求直线与双曲线的两个交点A,C的坐标和△AOC的面积。23. 如图,某农场要建一个长方形的养鸡场,鸡场的一边靠墙,墙长25m,另外三边用木栏围着,木栏长40m. (1)、若养鸡场面积为200m2 , 求鸡场平行于墙的一边长.(2)、养鸡场面积能达到250m2吗?如果能,请给出设计方案,如果不能,请说明理由.24. 如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
(1)、若养鸡场面积为200m2 , 求鸡场平行于墙的一边长.(2)、养鸡场面积能达到250m2吗?如果能,请给出设计方案,如果不能,请说明理由.24. 如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒. (1)、求直线AB的解析式;(2)、当t为何值时,△APQ与△AOB相似?(3)、当t为何值时,△APQ的面积为 个平方单位?
(1)、求直线AB的解析式;(2)、当t为何值时,△APQ与△AOB相似?(3)、当t为何值时,△APQ的面积为 个平方单位?