湖南省娄底市2018-2019学年九年级上学期数学期中考试试卷

试卷更新日期：2019-09-26 类型：期中考试

进入出卷网下载

一、单选题

1. 下列关于x的方程中，属于一元二次方程的是（）

A、x﹣1=0 B、x²+3x﹣5=0 C、x³+x=3 D、ax²+bx+c=0

查看试题解析
2. 已知函数y=（m﹣2） $x^{m^{2} - 5}$ 是反比例函数，则m的值为（）

A、2 B、﹣2 C、2或﹣2 D、任意实数

查看试题解析
3. 若反比例函数y= $\frac{k}{x}$ 的图象经过点(﹣1，﹣2)，则k的值为（）

A、﹣2 B、﹣1 C、1 D、2

查看试题解析
4. 下列图形一定是相似图形的是（　　）

A、两个矩形 B、两个正方形 C、两个直角三角形 D、两个等腰三角形

查看试题解析
5. 反比例函数y= $\frac{k}{x}$ 的图象如图，则函数y=﹣kx+2的图象可能是（）

A、 B、 C、 D、

查看试题解析
6. 如果x²﹣x﹣1=（x+1）⁰ ，那么x的值为（）

A、2或﹣1 B、0或1 C、2 D、﹣1

查看试题解析
7. 若点（﹣2，y₁），（﹣1，y₂），（3，y₃）在双曲线y= $\frac{k}{x}$ （k＜0）上，则y₁ ， y₂ ， y₃的大小关系是（）

A、y₁＜y₂＜y₃ B、y₃＜y₂＜y₁ C、y₂＜y₁＜y₃ D、y₃＜y₁＜y₂

查看试题解析
8. 关于 $x$ 的一元二次方程 $(m - 2) x^{2} + 2 x + 1 = 0$ 有实数根，则 $m$ 的取值范围是（）

A、 $m \leq 3$ B、 $m < 3$ C、 $m < 3 且 m \neq 2$ D、 $m \leq 3 且 m \neq 2$

查看试题解析
9. 如果两个相似三角形对应高的比是4：9，那么它们的面积比是（）

A、4：9 B、2：3 C、16：81 D、9：4

查看试题解析
10. A，B两城间的距离为15千米，一人行路的平均速度每小时不少于3千米，也不多于5千米，则表示此人由A到B的行路速度x（千米/小时）与所用时间y（小时）的关系y= $\frac{15}{x}$ 的函数图象是（）

A、 B、 C、 D、

查看试题解析
11. 如图，在正方形ABCD中，AD=6，点E是边CD上的动点（点E不与端点C，D重合），AE的垂直平分线FG分别交AD，AE，BC于点F，H，G．当 $\frac{F H}{H G} = \frac{1}{4}$ 时，DE的长为（）

A、2 B、 $\frac{12}{5}$ C、 $\frac{18}{5}$ D、4

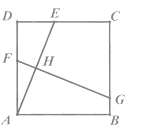查看试题解析

12. 观察下表，第（）个图形中“●”的个数与“★”的个数相等．

序号	1	2	3	…	n
图形				…	…
●的个数	8	16	24	…	…
★的个数	1	4	9	…	…

A、5 B、6 C、7 D、8

查看试题解析

二、填空题

13. 若反比例函数y＝ $\frac{2 a - 1}{x}$ 的图象有一支位于第一象限，则a的取值范围是．

查看试题解析
14. 已知 $\frac{x}{y}$ = $\frac{1}{3}$ ，则 $\frac{x - y}{y}$ 的值为．

查看试题解析
15. 菱形ABCD的一条对角线长为6，边AB的长是方程 $x^{2} - 7 x + 12 = 0$ 的一个根，则菱形ABCD的周长为．

查看试题解析
16. 如图，已知点C、D是线段AB的两个黄金分割点，若线段AB的长10厘米，则线段CD长厘米．

查看试题解析
17. 设m ， n是一元二次方程x²＋2x－7＝0的两个根，则m²＋3m＋n＝.

查看试题解析
18.
在平面直角坐标系中，点A（2，3），B（5，﹣2），以原点O为位似中心，位似比为1：2，把△ABO缩小，则点B的对应点B′的坐标是．

查看试题解析

三、解答题

19. 解方程：

(1)、 $x^{2} - 4 x - 1 = 0$

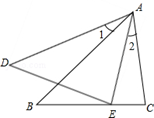
(2)、 ${(2 x + 3)}^{2} - 81 = 0$ ．

查看试题解析
20. 如图，AB•AE=AD•AC，且∠1=∠2，求证：△ABC∽△ADE．

查看试题解析
21. 为了方便孩子入学，小王家购买了一套学区房，交首付款15万元，剩余部分向银行贷款，贷款及贷款利息按月分期还款，每月还款数相同．计划每月还款y万元，x个月还清贷款，若y是x的反比例函数，其图象如图所示：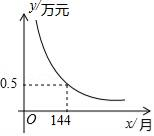

(1)、求y与x的函数解析式；

(2)、若小王家计划180个月（15年）还清贷款，则每月应还款多少万元？

查看试题解析
22. 已知关于x的方程 $x^{2} + a x + a - 2 = 0$ .

(1)、当该方程的一个根为1时，求a的值及该方程的另一根；

(2)、求证：不论a取何实数，该方程都有两个不相等的实数根.

查看试题解析
23. 某商场销售一批某品牌衬衫，衬衫进货单价为80元，销售单价为120元时，每天可售出20件．为了扩大销售，尽快减少库存，商场决定采取适当的降价措施．经调查发现，如果每件衬衫降价1元，商场平均每天就可多售出2件，若商场销售这种衬衫平均每天盈利1200元，售价应定为多少元？

查看试题解析
24. 如图，在平面直角坐标系中，过点M（0，2）的直线l与x轴平行，且直线l分别与反比例函数y= $\frac{6}{x}$ （x＞0）和y= $\frac{k}{x}$ （x＜0）的图象交于点P、点Q．

(1)、求点P的坐标；

(2)、若△POQ的面积为8，求k的值．

查看试题解析
25. 如图，一次函数y＝k₁x+b与反比例函数 $y = \frac{k_{2}}{x}$ 的图象交于A（2，m），B（n，﹣2）两点．过点B作BC⊥x轴，垂足为C，且S_△_ABC＝5．

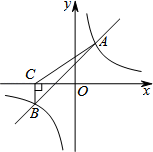(1)、求一次函数与反比例函数的解析式．

(2)、根据所给条件，请直接写出不等式k₁x+b＞ $\frac{k_{2}}{x}$ 的解集；

(3)、若P（p，y₁），Q（﹣2，y₂）是函数y＝ $\frac{k_{2}}{x}$ 图象上的两点，且y₁≥y₂ ，求实数p的取值范围．

查看试题解析
26. 如图，在矩形ABCD中，AB＝12cm，BC＝8cm．点E、F、G分别从点A、B、C同时出发，沿矩形的边按逆时针方向移动，点E、G的速度均为2cm/s，点F的速度为4cm/s，当点F追上点G(即点F与点G重合)时，三个点随之停止移动．设移动开始后第ts时，△E FG的面积为Scm² ．

(1)、当t＝1s时，S的值是多少？

(2)、写出S与t之间的函数解析式，并指出自变量t的取值范围；

查看试题解析