湖南省常德市鼎城区2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期:2019-09-26 类型:期中考试
一、单选题
-
1. 已知反比例函数y= 的图象经过点(2,3),那么下列四个点中,也在这个函数图象上的是( )A、(﹣6,1) B、(1,6) C、(2,﹣3) D、(3,﹣2)2. 若x1 , x2是一元二次方程x2-2x-3=0的两个根,则x1·x2的值是( )A、2 B、-2 C、4 D、-33. 如果实数m≠n,且 ,则m+n=( )A、7 B、8 C、9 D、104. 如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )
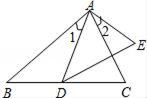 A、∠C=∠E B、∠B=∠ADE C、 D、5. 如图,双曲线y= 与直线y=﹣ x交于A、B两点,且A(﹣2,m),则点B的坐标是( )
A、∠C=∠E B、∠B=∠ADE C、 D、5. 如图,双曲线y= 与直线y=﹣ x交于A、B两点,且A(﹣2,m),则点B的坐标是( ) A、(2,﹣1) B、(1,﹣2) C、( ,﹣1) D、(﹣1, )6. 如图,在△ABC中,两条中线BE、CD相交于点O,则S△EOD∶S△BOC=( )
A、(2,﹣1) B、(1,﹣2) C、( ,﹣1) D、(﹣1, )6. 如图,在△ABC中,两条中线BE、CD相交于点O,则S△EOD∶S△BOC=( )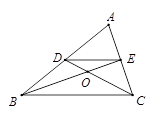 A、1﹕4 B、2﹕3 C、1﹕3 D、1﹕27. 如图,电线杆CD的高度为h,两根拉线AC与BC互相垂直(A、D、B在同一条直线上),设∠CAB=α,那么拉线BC的长度为( )
A、1﹕4 B、2﹕3 C、1﹕3 D、1﹕27. 如图,电线杆CD的高度为h,两根拉线AC与BC互相垂直(A、D、B在同一条直线上),设∠CAB=α,那么拉线BC的长度为( ) A、 B、 C、 D、8. 如图,在Rt△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC,则 的值为( )
A、 B、 C、 D、8. 如图,在Rt△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC,则 的值为( )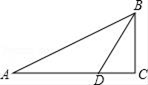 A、 B、3﹣ C、6﹣ D、
A、 B、3﹣ C、6﹣ D、二、填空题
-
9. 如图,为估算某河的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20m,EC=10m,CD=20m,则河的宽度AB=m.
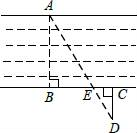 10. 如图,在△ABC中,∠C=90°,D是AC上一点,DE⊥AB于点E,若AC=8,BC=6,DE=3,则AD的长为 .
10. 如图,在△ABC中,∠C=90°,D是AC上一点,DE⊥AB于点E,若AC=8,BC=6,DE=3,则AD的长为 . 11. 如图,一山坡的坡度为i=1: ,小辰从山脚A出发,沿山坡向上走了200米到达点B,则小辰上升了米.
11. 如图,一山坡的坡度为i=1: ,小辰从山脚A出发,沿山坡向上走了200米到达点B,则小辰上升了米.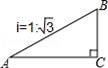 12. 如图,某地修建高速公路,要从B地向C地修一座隧道(B , C在同一水平上),某工程师乘坐热气球从B地出发,垂足上升100m到达A处,在A处观察C地的俯角为30°,则BC两地之间的距离为m .
12. 如图,某地修建高速公路,要从B地向C地修一座隧道(B , C在同一水平上),某工程师乘坐热气球从B地出发,垂足上升100m到达A处,在A处观察C地的俯角为30°,则BC两地之间的距离为m .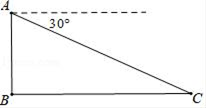 13. 小明家为响应节能减排号召,计划利用两年时间,将家庭每年人均碳排放量由目前的3125kg降至2000㎏﹙全球人均目标碳排放量﹚,则小明家未来两年人均碳排放量平均每年须降低的百分率是 .14. 在△ABC中,若 ,则∠C的度数是 .15. 如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1= (x>0)的图象上,顶点B在函数y2= (x>0)的图象上,∠ABO=30°,则 = .
13. 小明家为响应节能减排号召,计划利用两年时间,将家庭每年人均碳排放量由目前的3125kg降至2000㎏﹙全球人均目标碳排放量﹚,则小明家未来两年人均碳排放量平均每年须降低的百分率是 .14. 在△ABC中,若 ,则∠C的度数是 .15. 如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1= (x>0)的图象上,顶点B在函数y2= (x>0)的图象上,∠ABO=30°,则 = .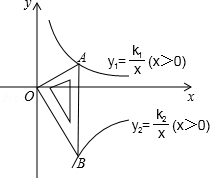
三、解答题
-
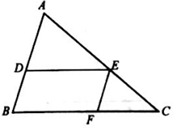
16. 解方程:x2﹣2x﹣1=0.17. 计算:cos45°•tan45°+ •tan30°﹣2cos60°•sin45°18. 如图,△ABC中,DE//BC,EF//A
B.求证:△ADE∽△EFC.
 19. 如图,在△ABC中,CD⊥AB,∠ACD=45°,∠DCB=60°,CD=40,求AB.
19. 如图,在△ABC中,CD⊥AB,∠ACD=45°,∠DCB=60°,CD=40,求AB.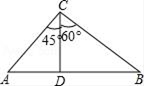 20. 如图,在13x13的网格图中,已知△ABC的顶点坐标分别为A(2,4)、B(3,2)、C(6,3).
20. 如图,在13x13的网格图中,已知△ABC的顶点坐标分别为A(2,4)、B(3,2)、C(6,3).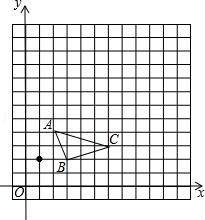 (1)、以点M(1,2)为位似中心,在第一象限把△ABC按相似比2:1放大,得△A'B'C',画出△ABC的位似图形;(2)、写出△A'B'C'的各顶点坐标.21. 如图,已知AE 平分∠BAC, .
(1)、以点M(1,2)为位似中心,在第一象限把△ABC按相似比2:1放大,得△A'B'C',画出△ABC的位似图形;(2)、写出△A'B'C'的各顶点坐标.21. 如图,已知AE 平分∠BAC, .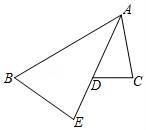 (1)、求证:∠E=∠C;(2)、若AB=9,AD=5,DC=3,求BE的长.22. 如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y= (x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.
(1)、求证:∠E=∠C;(2)、若AB=9,AD=5,DC=3,求BE的长.22. 如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y= (x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.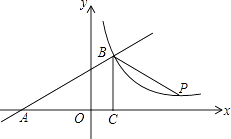 23. 为了维护国家主权和海洋权利,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在A处测得灯塔P在北偏东60°方向上,继续航行1小时到达B处,此时测得灯塔P在北偏东30°方向上.
23. 为了维护国家主权和海洋权利,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在A处测得灯塔P在北偏东60°方向上,继续航行1小时到达B处,此时测得灯塔P在北偏东30°方向上.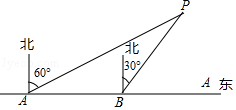 (1)、求∠APB的度数;(2)、已知在灯塔P的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?24. 某校为培育青少年科技创新能力,举办了动漫制作活动,小明设计了点做圆周运动的一个雏形,如图所示,甲、乙两点分别从直径的两端点A、B以顺时针、逆时针的方向同时沿圆周运动,甲运动的路程l(cm)与时间t(s)满足关系: (t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.
(1)、求∠APB的度数;(2)、已知在灯塔P的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?24. 某校为培育青少年科技创新能力,举办了动漫制作活动,小明设计了点做圆周运动的一个雏形,如图所示,甲、乙两点分别从直径的两端点A、B以顺时针、逆时针的方向同时沿圆周运动,甲运动的路程l(cm)与时间t(s)满足关系: (t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.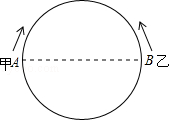 (1)、甲运动4s后的路程是多少?(2)、甲、乙从开始运动到第一次相遇时,它们运动了多少时间?(3)、甲、乙从开始运动到第二次相遇时,它们运动了多少时间?25. 已知点E、F分别是四边形ABCD边AB、AD上的点,且DE与CF相交于点G.
(1)、甲运动4s后的路程是多少?(2)、甲、乙从开始运动到第一次相遇时,它们运动了多少时间?(3)、甲、乙从开始运动到第二次相遇时,它们运动了多少时间?25. 已知点E、F分别是四边形ABCD边AB、AD上的点,且DE与CF相交于点G.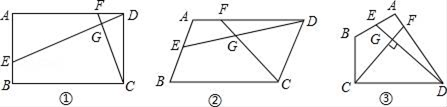 (1)、如图①,若AB∥CD,AB=CD,∠A=90°,且AD•DF=AE•DC,求证:DE⊥CF:(2)、如图②,若AB∥CD,AB=CD,且∠A=∠EGC时,求证:DE•CD=CF•DA:(3)、如图③,若BA=BC=3,DA=DC=4,设DE⊥CF,当∠BAD=90°时,试判断 是否为定值,并证明.
(1)、如图①,若AB∥CD,AB=CD,∠A=90°,且AD•DF=AE•DC,求证:DE⊥CF:(2)、如图②,若AB∥CD,AB=CD,且∠A=∠EGC时,求证:DE•CD=CF•DA:(3)、如图③,若BA=BC=3,DA=DC=4,设DE⊥CF,当∠BAD=90°时,试判断 是否为定值,并证明.