江西省2019年中考数学试卷
试卷更新日期:2019-09-26 类型:中考真卷
一、单选题
-
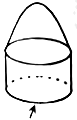
1. 2的相反数是( )A、 B、 C、 D、2. 计算 的结果为( )A、 B、 C、 D、3. 如图是手提水果篮抽象的几何体,以箭头所指的方向为主视图方向,则它的俯视图为( )
 A、
A、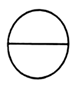 B、
B、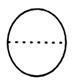 C、
C、 D、
D、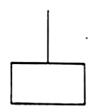 4. 根据《居民家庭亲子阅读消费调查报告》中的相关数据制成扇形统计图,由图可知,下列说法错误的是( )
4. 根据《居民家庭亲子阅读消费调查报告》中的相关数据制成扇形统计图,由图可知,下列说法错误的是( ) A、扇形统计图能反映各部分在总体中所占的百分比 B、每天阅读30分钟以上的居民家庭孩子超过50% C、每天阅读1小时以上的居民家庭孩子占20% D、每天阅读30分钟至1小时的居民家庭孩子对应扇形的圆心角是108°5. 已知正比例函数 的图象与反比例函数 图象相交于点 ,下列说法正确的是( )A、反比例函数 的解析式是 B、两个函数图象的另一交点坐标为 C、当 或 时, D、正比例函数 与反比例函数 都随 的增大而增大6. 如图,由10根完全相同的小棒拼接而成,请你再添2根与前面完全相同的小棒,拼接后的图形恰好有3个菱形的方法共有( )
A、扇形统计图能反映各部分在总体中所占的百分比 B、每天阅读30分钟以上的居民家庭孩子超过50% C、每天阅读1小时以上的居民家庭孩子占20% D、每天阅读30分钟至1小时的居民家庭孩子对应扇形的圆心角是108°5. 已知正比例函数 的图象与反比例函数 图象相交于点 ,下列说法正确的是( )A、反比例函数 的解析式是 B、两个函数图象的另一交点坐标为 C、当 或 时, D、正比例函数 与反比例函数 都随 的增大而增大6. 如图,由10根完全相同的小棒拼接而成,请你再添2根与前面完全相同的小棒,拼接后的图形恰好有3个菱形的方法共有( ) A、3种 B、4种 C、5种 D、6种
A、3种 B、4种 C、5种 D、6种二、填空题
-
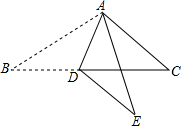
7. 因式分解: .8. 我国古代数学名著(孙子算经)有估算方法:“方五,邪(通“斜”)七。见方求邪,七之,五而一。”译文为:如果正方形的边长为五,则它的对角线长为七.已知正方形的边长,求对角线长,则先将边长乘以七再除以五.若正方形的边长为1,由勾股定理得对角线长为 ,依据《孙子算经》的方法,则它的对角线的长是 .9. 设 , 是一元二次方程 的两根,则 .10. 如图,在 中,点 是 上的点, ,将 沿着 翻折得到 ,则 °.
 11. 斑马线前“车让人”,不仅体现着一座城市对生命的尊重,也直接反映着城市的文明程度.如图,某路口的斑马线路段 横穿双向行驶车道,其中 米,在绿灯亮时,小明共用11秒通过 ,其中通过 的速度是通过 速度的1.2倍,求小明通过 时的速度.设小明通过 时的速度是 米/秒,根据题意列方程得: .
11. 斑马线前“车让人”,不仅体现着一座城市对生命的尊重,也直接反映着城市的文明程度.如图,某路口的斑马线路段 横穿双向行驶车道,其中 米,在绿灯亮时,小明共用11秒通过 ,其中通过 的速度是通过 速度的1.2倍,求小明通过 时的速度.设小明通过 时的速度是 米/秒,根据题意列方程得: .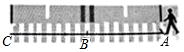 12. 在平面直角坐标系中, 三点的坐标分别为 , , ,点 在 轴上,点 在直线 上,若 , 于点 ,则点 的坐标为 .
12. 在平面直角坐标系中, 三点的坐标分别为 , , ,点 在 轴上,点 在直线 上,若 , 于点 ,则点 的坐标为 .三、解答题
-
13.(1)、计算: ;(2)、如图,四边形 中, , ,对角线 , 相交于点 ,且 .
求证:四边形 是矩形.
 14. 解不等式组: 并在数轴上表示它的解集.
14. 解不等式组: 并在数轴上表示它的解集. 15. 在中, , 点在以为直径的半圆内.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).(1)、在图1中作弦 ,使 ;
15. 在中, , 点在以为直径的半圆内.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).(1)、在图1中作弦 ,使 ; (2)、在图2中以 为边作一个45°的圆周角.
(2)、在图2中以 为边作一个45°的圆周角.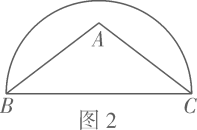 16. 为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.(1)、八(1)班抽中歌曲《我和我的祖国》的概率是;(2)、试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.17. 如图,在平面直角坐标系中,点 的坐标分别为 , ,连接 ,以 为边向上作等边三角形 .
16. 为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.(1)、八(1)班抽中歌曲《我和我的祖国》的概率是;(2)、试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.17. 如图,在平面直角坐标系中,点 的坐标分别为 , ,连接 ,以 为边向上作等边三角形 . (1)、求点 的坐标;(2)、求线段 所在直线的解析式.18. 某校为了解七、八年级学生英语听力训练情况(七、八年级学生人数相同),某周从这两个年级学生中分别随机抽查了30名同学,调查了他们周一至周五的听力训练情况,根据调查情况得到如下统计图表:周一至周五英语听力训练人数统计表
(1)、求点 的坐标;(2)、求线段 所在直线的解析式.18. 某校为了解七、八年级学生英语听力训练情况(七、八年级学生人数相同),某周从这两个年级学生中分别随机抽查了30名同学,调查了他们周一至周五的听力训练情况,根据调查情况得到如下统计图表:周一至周五英语听力训练人数统计表年级
参加英语听力训练人数
周一
周二
周三
周四
周五
七年级
15
20
30
30
八年级
20
24
26
30
30
合计
35
44
51
60
60
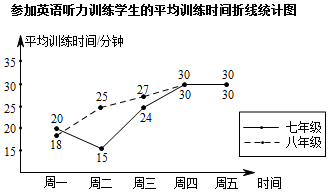 (1)、填空: ;(2)、根据上述统计图表完成下表中的相关统计量:
(1)、填空: ;(2)、根据上述统计图表完成下表中的相关统计量:年级
平均训练时间的中位数
参加英语听力训练人数的方差
七年级
24
34
八年级
14.4
(3)、请你利用上述统计图表,对七、八年级英语听力训练情况写出两条合理的评价;(4)、请你结合周一至周五英语听力训练人数统计表,估计该校七、八年级共480名学生中周一至周五平均每天有多少人进行英语听力训练.19. 如图1, 为半圆的直径,点 为圆心, 为半圆的切线,过半圆上的点 作 交 于点 ,连接 .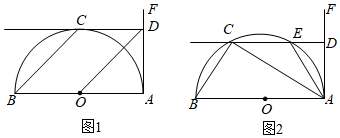 (1)、连接 ,若 ,求证: 是半圆的切线;(2)、如图2,当线段 与半圆交于点 时,连接 , ,判断 和 的数量关系,并证明你的结论.20. 图1是一台实物投影仪,图2是它的示意图,折线 表示固定支架, 垂直水平桌面 于点 ,点 为旋转点, 可转动,当 绕点 顺时针旋转时,投影探头 始终垂直于水平桌面 ,经测量: , , , .(结果精确到0.1)
(1)、连接 ,若 ,求证: 是半圆的切线;(2)、如图2,当线段 与半圆交于点 时,连接 , ,判断 和 的数量关系,并证明你的结论.20. 图1是一台实物投影仪,图2是它的示意图,折线 表示固定支架, 垂直水平桌面 于点 ,点 为旋转点, 可转动,当 绕点 顺时针旋转时,投影探头 始终垂直于水平桌面 ,经测量: , , , .(结果精确到0.1)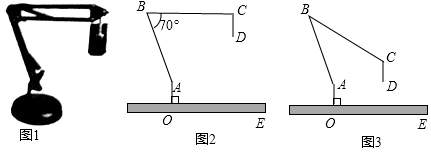 (1)、如图2, , .
(1)、如图2, , .①填空: °;
②求投影探头的端点 到桌面 的距离 .
(2)、如图3,将(1)中的 向下旋转,当投影探头的端点 到桌面 的距离为 时,求 的大小.(参考数据: , , , )21. 数学活动课上,张老师引导同学进行如下探究:如图1,将长为 的铅笔 斜靠在垂直于水平桌面 的直尺 的边沿上,一端 固定在桌面上,图2是示意图.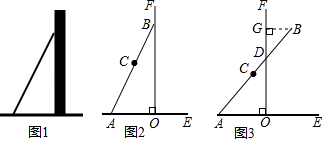
(1)、活动一如图3,将铅笔 绕端点 顺时针旋转, 与 交于点 ,当旋转至水平位置时,铅笔 的中点 与点 重合.
数学思考
设 ,点 到 的距离 .
①用含 的代数式表示: 的长是 , 的长是 ;
② 与 的函数关系式是 , 自变量 的取值范围是 .
(2)、活动二①列表:根据(1)中所求函数关系式计算并补全表格.
6
5
4
3.5
3
2.5
2
1
0.5
0
0
0.55
1.2
1.58
1.0
2.47
3
4.29
5.08
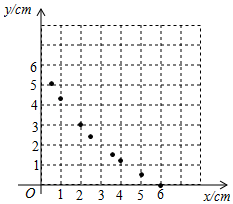
②描点:根据表中数值,描出①中剩余的两个点 .
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
数学思考
(3)、请你结合函数的图象,写出该函数的两条性质或结论.22. 在图1,2,3中,已知 , ,点 为线段 上的动点,连接 ,以 为边向上作菱形 ,且 .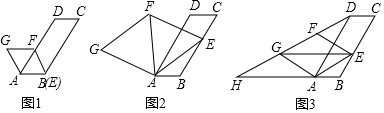 (1)、如图1,当点 与点 重合时, °;(2)、如图2,连接 .
(1)、如图1,当点 与点 重合时, °;(2)、如图2,连接 .①填空: (填“>”,“<”,“=”);
(3)、如图3,连接 , ,并延长 交 的延长线于点 ,当四边形 是平行四边形时,求 的值.