初中数学华师大版八年级上学期 第11章测试卷
试卷更新日期:2019-09-26 类型:单元试卷
一、单选题
-
1. 若a2=(-5)2 , b3=(-5)3 , 则a+b的值是( )A、0或-10或10 B、0或-10 C、-10 D、02. 下列各式正确的是( )A、 = ±3 B、 = ±3 C、 =3 D、 =-33. 一个正数的平方根是2m+3和m+1,则这个数为( )A、﹣ B、 C、 D、1或4. 下列各数中,没有平方根的是( )A、
 B、
B、 C、
C、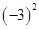 D、
D、 5. 若2m﹣4与3m﹣1是同一个数的平方根,则这个数可能是( )
5. 若2m﹣4与3m﹣1是同一个数的平方根,则这个数可能是( )
A、2 B、﹣2 C、4 D、16. 下列实数中最大的是( )A、 B、 C、 D、7. 小明学了在数轴上画出表示无理数的点的方法后,进行练习:首先画数轴,原点为O,在数轴上找到表示数2的点A,然后过点A作AB⊥OA,使AB=3(如图).以O为圆心,OB的长为半径作弧,交数轴正半轴于点P,则点P所表示的数介于( ) A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间
A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间二、填空题
-
8. 实数3的算术平方根是 .9. 的算术平方根是 , 的立方根是。
三、计算题
-
10. 计算:(-1)2+( )2-(-9)+(-6)÷2.11.(1)、计算: +| ﹣2|﹣ + ﹣(2)、一个正数的平方根是2x+4和﹣3x﹣2,求这个数的立方根.
四、综合题