浙江省台州市2019-2020学年八年级上学期数学开学试卷
试卷更新日期：2019-09-24 类型：开学考试
一、选择题（每小题3分，共30分）
-
1. 在下列各图形中，分别画出了△ABC中BC边上的高AD，其中正确的是 （ ）A、
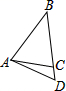B、
C、
D、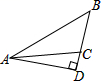
2. 正十边形的每一个内角的度数为（ ）.A、120° B、135° C、140° D、144°3. 下列数据能唯一确定三角形的形状和大小的是（ ）A、AB=4，BC=5，∠C=60° B、AB=6，∠C=60°，∠B=70° C、AB=4，BC=5，CA=10 D、∠C=60°，∠B=70°，∠A=50°4. 用直尺和圆规作一个角的平分线如图所示，说明∠AOC＝∠BOC的依据是（ ）．
A、SSS B、ASA C、AAS D、角平分线上的点到角两边距离相等5. 下列语句中，正确的是（ ）A、三角形的外角大于任何一个内角 B、三角形的外角等于这个三角形的两个内角之和 C、三角形的外角中，至少有两个钝角 D、三角形的外角中，至少有一个钝角6. 已知△ABC的三边长为a，b，c，化简|a＋b－c|－|b－a－c|的结果是（ ）A、2b－2c B、－2b C、2a＋2b D、2a7. 三个全等三角形按如图的形式摆放，则∠1+∠2+∠3的度数是（ ）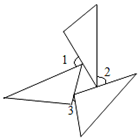
A、90° B、120° C、135° D、180°8. 如图，三角形纸片ABC中，∠A=80°，∠B=60°，将纸片的角折叠，使点C落在△ABC内，若∠α=30°，则∠β的度数是（ ）
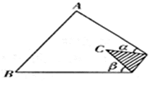A、 B、 C、 D、9. 如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE=DF，连结BF，CE.下列说法：①△ABD和△ACD面积相等；②∠BAD=∠CAD；③△BDF≌△CDE；④BF∥CE；其中正确的有（ ）
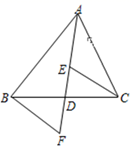A、1个 B、2个 C、3个 D、4个10. 如图，在△ABC中，BD、BE分别是高和角平分线，点F在CA的延长线上，FH⊥BE交BD于G，交BC于H，下列结论：①∠DBE=∠F；②2∠BEF=∠BAF+∠C；③∠F= （∠BAC﹣∠C）；④∠BGH=∠ABE+∠C.其中正确的是（ ）
A、①②③ B、①③④ C、①②④ D、①②③④二、填空题（每小题3分，共18分）
-
11. 如图，一扇窗户打开后，用窗钩AB可将其固定，这里所运用的几何原理是 ．
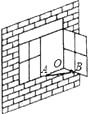12. 将两张三角形纸片如图摆放，量得∠1+∠2+∠3+∠4=220°，则∠5的度数为.
13. 如图，在△ABC中，已知点D、E、F分别为BC、AD、CE的中点，且 =4cm2 ， 则 = ．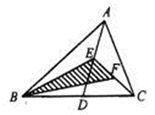
14. 如图，在 中， ， ，点C的坐标为 (-2，0)，点A的坐标为(-8，3)，点B的坐标是 ．
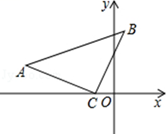15. 如图所示，△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P，若∠BPC＝40°，则∠CAP＝ ．
16. 如图，在△ABC中，∠C=90°，BC=8cm，AC=6cm，点E是BC的中点，动点P从A点出发，先以每秒2cm的速度沿A→C运动，然后以1cm/s的速度沿C→B运动．若设点P运动的时间是t秒，那么当t= ， △APE的面积等于6．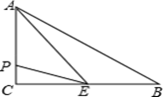
三、解答题（本题8小题，共72分）
-
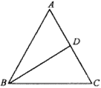
17. 如图，△ABC中，AB=AC，D为AC的中点，△ABD的周长比△BDC的周长大2，且BC的边长是方程的 解，求△ABC三边的长．
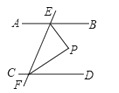
18.如图，已知AB∥CD，EF与AB、CD分别相交于点E、F，∠BEF与∠EFD的平分线相交于点P，求证：EP⊥FP．
19. 如图，已知点E、C在线段BF上，BE=CF，∠ACB=∠F，AC=DF．求证：AB∥DE。
20. △ABC中，AD⊥BC于点D，BE是∠ABC的平分线，已知∠ABC=40°，∠C=60°，求∠AOB的度数 。
21. 如图，已知在四边形ABCD中，点E在AD上，∠BAC＝∠D，∠B+∠AEC＝180°，BC＝CE．求证：AC=DC．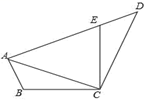
22. 如图，△ABC≌△ADE，已知点C和点E是对应点，BC的延长线分别交AD，DE于点F，G，且∠DAC=10°，∠B＝∠D=25°，∠EAB=120°，试求∠DFB和∠DGB的度数．
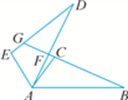23. 如图，△OAB和△OCD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝α，AC、BD交于M.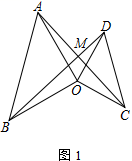
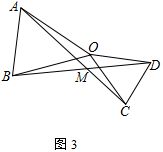(1)、如图1，当α＝90°时，∠AMD的度数为(2)、如图2，当α＝60°时，∠AMD的度数为.(3)、如图3，当△OCD绕O点任意旋转时，∠AMD与α是否存在着确定的数量关系？如果存在，请你用表示∠AMD，并用图3进行证明；若不确定，说明理由.24. 如图(1)， 已知△ABC中， ∠BAC=900 ， AB=AC， AE是过A的一条直线， 且B.C在A.E的异侧， BD⊥AE于D， CE⊥AE于E
(1)、试说明：BD=DE+CE.(2)、若直线AE绕A点旋转到图(2)位置时，其余条件不变，请直接写出BD与DE.CE的数量关系？不需说明理由(3)、如图(3)若将图（2）中的AB=AC改为∠ABD=∠ABC其余条件不变，问AD与AE的数量关系如何? 并说明理由.