浙江省杭州市萧山区城厢片五校2020届九年级上学期数学开学试卷

试卷更新日期：2019-09-24 类型：开学考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. $| - \sqrt{3} |$ =（）

A、 $\sqrt{3}$ B、 $- \sqrt{3}$ C、 $\frac{\sqrt{3}}{3}$ D、 $- \frac{\sqrt{3}}{3}$

查看试题解析
2. 下列各式正确的是（）

A、 $\sqrt{16} = \pm 4$ B、 $\sqrt{16 \frac{1}{9}} = 4 \frac{1}{3}$ C、 $\sqrt{16} = 4$ D、 $\sqrt{- 16} = - 4$

查看试题解析
3. 若关于x的分式 $\frac{x - 1}{x^{2} - 4 x + a}$ ，当x=1时其值为0,则实数a的取值范围（）

A、a≠0 B、a＞3 C、a＞0 D、a≠3

查看试题解析
4. 为了考察甲、乙两块地小麦的长势，分别从中抽取10株苗，测得苗高如下（单位：cm）：
甲：12,13,14,15,10,16,13,11,15,11；乙：11,16,17,14,13,19,6,8,10,16.

要比较哪块地小麦长得比较整齐，我们应选择的统计量是（）

A、中位数 B、平均数 C、众数 D、方差

查看试题解析
5. 在▱ABCD中，∠C、∠D的度数之比为3∶1，则 ∠A等于（）

A、45° B、50° C、135° D、130°

查看试题解析
6. 已知y＝0是关于y的一元二次方程（m﹣1）y²+my+4m²﹣4＝0的一个根，那么m的值是（）

A、﹣1 B、±1 C、1 D、0

查看试题解析
7. 一件毛衣先按成本提高50%标价，再以8折出售，获利28元，求这件毛衣的成本是多少元.若设成本是x元，可列方程为（）

A、0.8x+28＝（1+50%）x B、0.8x﹣28＝（1+50%）x C、x+28＝0.8×（1+50%）x D、x﹣28＝0.8×（1+50%）x

查看试题解析
8. 如图，直线y=mx与双曲线 $y = \frac{k}{x}$ 交于A、B两点，过点A作AM⊥x轴，垂足为M，连结BM，若S_△ABM=2，则k的值是（）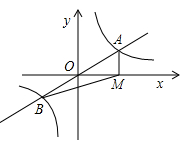

A、m B、m-2 C、2 D、4

查看试题解析
9. 如图，在菱形ABCD中，∠A是锐角，E为边AD上一点，△ABE沿着BE折叠，使点A的对应点F恰好落在边CD上，连接EF，BF，给出下列结论：①若∠A＝70°，则∠ABE＝35°；②若点F是CD的中点，则S_△ABE＝ $\frac{1}{3}$ S_菱形ABCD ．下列判断正确的是（）

A、①错，②对 B、①对，②错 C、①，②都错 D、①，②都对

查看试题解析
10. 如图，在平面直角坐标系中，正方形ABCD的顶点A的坐标为（﹣1，1），点B在x轴正半轴上，点D在第三象限的双曲线 $y = \frac{8}{x}$ 上，过点C作CE∥x轴交双曲线于点E，则CE的长为（）

A、 $\frac{8}{5}$ B、 $\frac{23}{5}$ C、3.5 D、5

查看试题解析

二、选择题（每题4分，共24分）

11. 分解因式：3x（x﹣2）﹣（2﹣x）＝．

查看试题解析
12. 如图，BC//DE.若∠A=30°，∠C=20°，则∠E=.

查看试题解析
13. 设点A（x₁ ， y₁），B(x₂ ， y₂)位于函数 $y = \frac{k}{x}$ . 的图像上，当x₁ >x₂>0必有0<y₁ <y₂ ，则k0.(选“>”，“<”，“=”中的一个填写)

查看试题解析
14. 使代数式 $（ x - 4 ）^{- 1}$ 有意义的x的取值范围是.

查看试题解析
15. 如图，已知双曲线 $y = \frac{k}{x}$ （ $x > 0$ ）经过矩形OABC的边AB，BC的中点F，E，且四边形OEBF的面积为2，则k= ．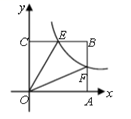

查看试题解析
16. 已知△ABC与△ABD不全等，且AC=AD=1，∠ABD=∠ABC=45°，∠ACB=60°，则CD= ．

查看试题解析

三、解答题（本题有7小题，共66分）

17. 计算

(1)、 $\sqrt{18} - 4 \sqrt{\frac{1}{2}} + \sqrt{24} \div \sqrt{3}$

(2)、已知 $x = \sqrt{5} - 1$ ,求代数式 $x^{2} + 2 x - 3$ 的值.

查看试题解析
18. 已知面积为30的菱形ABCD（顺时针排列）的顶点坐标分别为A（1，-2），B（a，b），C（1，4），D（c，d），求a，b，c，d的值及菱形的周长．

查看试题解析
19. 为了了解某校新初三暑期阅读课外书的情况，某研究小组随机采访该校新九年级的20位同学，得到这20位同学暑期读课外书册数的统计如下：

册数

0

2

3

5

6

8

10

人数

1

2

4

8

2

2

1

(1)、这20位同学暑期看课外书册数的中位数是册，众数是册，平均数是册。

(2)、若小明同学把册数中的数据“8”看成了“7”，那么中位数，众数，平均数中不受影响的是。

(3)、若该校有600名新初三学生，试估计该校新初三学生暑期阅读课外书的总册数。

查看试题解析
20. 已知在四边形ABCD中，AB=CD，∠BAE=∠DCF，∠AEF=∠EFC，求证：四边形AECF是平行四边形，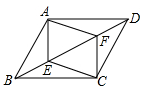

查看试题解析
21. 如图，已知一次函数y＝ax + b（a，b为常数，a≠0）的图象与x轴，y轴分别交于点A，B，且与反比例函数 $y = \frac{k}{x}$ （k为常数，k≠0）的图象在第二象限内交于点C，作CD⊥x轴于点D，若OA＝OD＝ $\frac{3}{4}$ OB＝3．

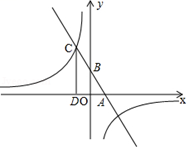(1)、求一次函数与反比例函数的解析式；

(2)、观察图象直接写出不等式0＜ax + b≤ $\frac{k}{x}$ 的解集．

查看试题解析
22. 已知△ABC的一条边BC的长为5，另两边AB，AC的长分别为关于x的一元二次方程 $x^{2} - (2 k + 3) x + k^{2} + 3 k + 2 = 0$ 的两个实数根。

(1)、无论k为何值，方程总有两个不相等的实数根；

(2)、当k=2时，请判断△ABC的形状并说明理由；

(3)、k为何值时，△ABC是等腰三角形，并求△ABC的周长。

查看试题解析
23. 已知△ABD与△GDF都是等腰直角三角形，BD与DF均为斜边（BD＜DF）．

(1)、如图1，B，D，F在同一直线上，过F作MF⊥GF于点F，取MF=AB，连结AM交BF于点H，连结GA，GM．
①求证：AH=HM；

②请判断△GAM的形状，并给予证明；

③请用等式表示线段AM，BD，DF的数量关系，并说明理由．

(2)、如图2，GD⊥BD，连结BF，取BF的中点H，连结AH并延长交DF于点M，请用等式直接写出线段AM，BD，DF的数量关系．

查看试题解析

册数	0	2	3	5	6	8	10
人数	1	2	4	8	2	2	1