浙江省杭州市萧山城北初中2020届九年级上学期数学开学试卷
试卷更新日期:2019-09-24 类型:开学考试
一、选择题 (本大题共10小题,每小题3分,共30分)
-
1. 用科学记数法表示316000000为( )A、3.16×107 B、3.16×108 C、31.6×107 D、31.6×1062. 下列图形中,轴对称图形是( )A、
 B、
B、 C、
C、 D、
D、 3. 下面说法正确的是( )A、(2ab)2=2a2b2 B、(a+b)2=a2+b2 C、a5+b5=2a10 D、a(a2+1)=a3+a4. 如图所示,在△ABC中,M是BC的中点,AN平分∠BAC,BN⊥AN.若AB=14,AC=20,则MN的长为( )
3. 下面说法正确的是( )A、(2ab)2=2a2b2 B、(a+b)2=a2+b2 C、a5+b5=2a10 D、a(a2+1)=a3+a4. 如图所示,在△ABC中,M是BC的中点,AN平分∠BAC,BN⊥AN.若AB=14,AC=20,则MN的长为( )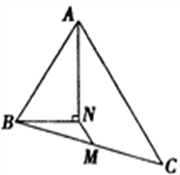 A、2 B、2.5 C、3 D、3.55. 如图,OE是∠AOB的平分线,BD⊥OA于点D,AC⊥ BO于点C,则图中全等的三角形共有( )
A、2 B、2.5 C、3 D、3.55. 如图,OE是∠AOB的平分线,BD⊥OA于点D,AC⊥ BO于点C,则图中全等的三角形共有( )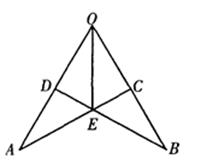 A、2对 B、3对 C、4对 D、5对6. “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )
A、2对 B、3对 C、4对 D、5对6. “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )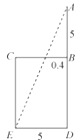 A、1.25 尺 B、57.5 尺 C、6.25 尺 D、56.5 尺7. 一次函数y1=kx+b与y2=x+a的图象如图所示,有下列结论:①k<0;②a>0;③当x<3时,y1<y2.其中正确结论的个数是( )
A、1.25 尺 B、57.5 尺 C、6.25 尺 D、56.5 尺7. 一次函数y1=kx+b与y2=x+a的图象如图所示,有下列结论:①k<0;②a>0;③当x<3时,y1<y2.其中正确结论的个数是( )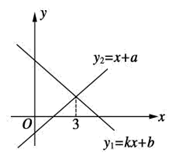 A、0个 B、1个 C、2个 D、3个8. 某中学规定学生的学期体育成绩满分为100分,其中课外体育占20%,期中考试成绩占30%,期末考试成绩占50%.小彤的这三项成绩(百分制)分别为95分,90分,88分,则小彤这学期的体育成绩为( )A、89分 B、90分 C、92分 D、93分9. 如图,在▱ABCD中,BE⊥AD于点E,BF⊥CD于点F,若BE=2,BF=3,▱ABCD的周长为20,则平行四边形的面积为( )
A、0个 B、1个 C、2个 D、3个8. 某中学规定学生的学期体育成绩满分为100分,其中课外体育占20%,期中考试成绩占30%,期末考试成绩占50%.小彤的这三项成绩(百分制)分别为95分,90分,88分,则小彤这学期的体育成绩为( )A、89分 B、90分 C、92分 D、93分9. 如图,在▱ABCD中,BE⊥AD于点E,BF⊥CD于点F,若BE=2,BF=3,▱ABCD的周长为20,则平行四边形的面积为( )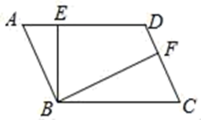 A、12 B、18 C、20 D、2410. 甲、乙两家商场平时以同样价格出售相同的商品,春节期间两家商场都让利酬宾,如图是购买甲、乙两家商场该商品的实际金额 、 (元)与原价 (元)的函数图象,下列说法正确的是( )
A、12 B、18 C、20 D、2410. 甲、乙两家商场平时以同样价格出售相同的商品,春节期间两家商场都让利酬宾,如图是购买甲、乙两家商场该商品的实际金额 、 (元)与原价 (元)的函数图象,下列说法正确的是( )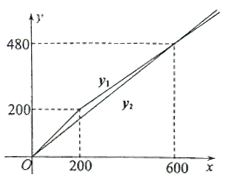 A、当 时,选甲更省钱 B、当 时,甲、乙实际金额一样 C、当 时,选乙更省钱 D、当 时,选甲更省钱
A、当 时,选甲更省钱 B、当 时,甲、乙实际金额一样 C、当 时,选乙更省钱 D、当 时,选甲更省钱二、填空题 (本大题共6个小题,每小题4分,共24分)
-
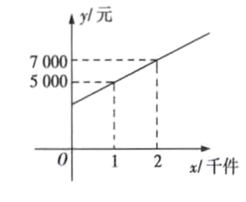
11. 已知a,b,c都是有理数,且满足 ,则 .12. 函数 中,自变量 的取值范围是 .13. 不等式 的解集是 .14. 若关于x的一次函数y=(m+1)x+2m﹣3的图象经过第一、三、四象限,则m的取值范围为 .15. 如图是某公司一销售人员的个人月收入y(元)与其每月的销售量x(千件)的函数关系图象,则当此销售人员的销售量为4千件时,月收入是元.
 16. 如图,已知在 中, ,点 是 延长线上的一点, ,点 是 上一点, ,连接 , 、 分别是 、 的中点,则 .
16. 如图,已知在 中, ,点 是 延长线上的一点, ,点 是 上一点, ,连接 , 、 分别是 、 的中点,则 .
三、解答题 (本大题共7个小题,共66分)
-
17. 先化简,再求值: ,其中 , .18. 如图,已知平行四边形 ,延长 到 ,使 ,连接 与 交于 点.
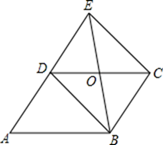 (1)、求证: ;(2)、当 时,连续 , ,求证:四边形 为矩形.19. 某农机租赁公司共有50台收割机,其中甲型20台、乙型30台,现将这50台联合收割机派往A,B两地区收割小麦,其中30台派往A地区,20台派往B地区,两地区与该农机公司商定的每天租赁价格如下表:
(1)、求证: ;(2)、当 时,连续 , ,求证:四边形 为矩形.19. 某农机租赁公司共有50台收割机,其中甲型20台、乙型30台,现将这50台联合收割机派往A,B两地区收割小麦,其中30台派往A地区,20台派往B地区,两地区与该农机公司商定的每天租赁价格如下表:每台甲型收割机的租金
每台乙型收割机的租金
A地区
1800元
1600元
B地区
1600元
1200元
(1)、设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机天获得的租金为y元,求y关于x的函数关系式,并写出自变量的取值范围:(2)、若使农机租赁公司这50台收割机一天所获租金不低于79600元,为农机租赁公司拟出一个分派方案,使该公司50台收割机每天获得租金最高,并说明理由.20. 如图,已知 ,现将一直角三角形PMN放入图中,其中 ,PM交AB于点E,PN交CD于点F.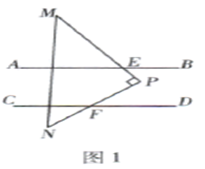
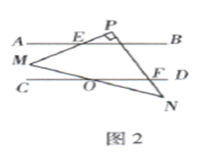 (1)、当 在如图2所示的位置时,求证: ;(2)、在(1)的条件下,若MN与CD交于点O,且 , ,求 的度数。21. 如图,已知直线 分别与x轴、y轴交于点A,B,直线 分别与x轴、y轴交于点C,D,且直线 与 相交于点P, .
(1)、当 在如图2所示的位置时,求证: ;(2)、在(1)的条件下,若MN与CD交于点O,且 , ,求 的度数。21. 如图,已知直线 分别与x轴、y轴交于点A,B,直线 分别与x轴、y轴交于点C,D,且直线 与 相交于点P, .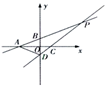 (1)、求b的值和点P的坐标;(2)、求 的面积.22. 如图,已知直线AB与正比例函数 的图象交于点 ,与y轴交于点 .点P为直线OA上的动点,点P的横坐标为t,以点P为顶点,作长方形PDEF,满足 轴,且 , .
(1)、求b的值和点P的坐标;(2)、求 的面积.22. 如图,已知直线AB与正比例函数 的图象交于点 ,与y轴交于点 .点P为直线OA上的动点,点P的横坐标为t,以点P为顶点,作长方形PDEF,满足 轴,且 , .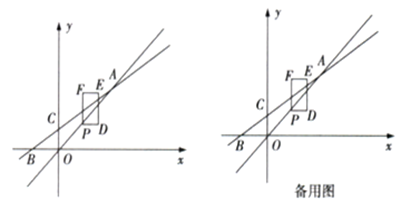 (1)、求k的值及直线AB的函数表达式,并判定 时,点E是否落在直线AB上;(2)、在点P运动的过程中,当点F落在直线AB上时,求t的值;(3)、在点P运动的过程中,若长方形PDEF与直线AB有公共点,求t的取值范围.23. 如图, 是正方形 的边 上的动点, 是边 延长线上的一点,且 , ,设 , .
(1)、求k的值及直线AB的函数表达式,并判定 时,点E是否落在直线AB上;(2)、在点P运动的过程中,当点F落在直线AB上时,求t的值;(3)、在点P运动的过程中,若长方形PDEF与直线AB有公共点,求t的取值范围.23. 如图, 是正方形 的边 上的动点, 是边 延长线上的一点,且 , ,设 , .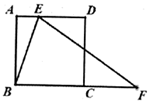
 (1)、当 是等边三角形时,求 的长;(2)、求 与 的函数解析式,并写出它的自变量取值范围;(3)、把 沿着直线 翻折,点 落在点 处,试探索: 能否为等腰三角形?如果能,请求出 的长;如果不能,请说明理由.
(1)、当 是等边三角形时,求 的长;(2)、求 与 的函数解析式,并写出它的自变量取值范围;(3)、把 沿着直线 翻折,点 落在点 处,试探索: 能否为等腰三角形?如果能,请求出 的长;如果不能,请说明理由.