2016-2017学年山东省日照市莒县七年级下学期期中数学试卷
试卷更新日期:2017-06-28 类型:期中考试
一、选择题
-
1. 如图,∠1和∠2是对顶角的是( )A、
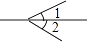 B、
B、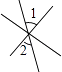 C、
C、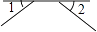 D、
D、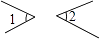 2. 点P(﹣1,5)所在的象限是( )
2. 点P(﹣1,5)所在的象限是( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 实数 ,﹣ ,0.1010010001, ,π, 中,无理数的个数是( )A、1 B、2 C、3 D、44. 下列不属于二元一次方程组的是( )A、 B、 C、 D、5. 如图.已知AB∥CD,∠1=70°,则∠2的度数是( )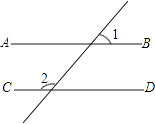 A、60° B、70° C、80° D、1106. 如果一个角的两边和另一个角的两边互相平行,那么这两个角之间关系为( )
A、60° B、70° C、80° D、1106. 如果一个角的两边和另一个角的两边互相平行,那么这两个角之间关系为( )
A、相等 B、互补 C、相等或互补 D、不能确定7. 下列说法正确的是( )A、﹣5是﹣25的平方根 B、3是(﹣3)2的算术平方根 C、(﹣2)2的平方根是2 D、8的平方根是±48. 如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC:∠EOD=1:2,则∠BOD等于( )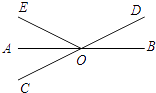 A、30° B、36° C、45° D、72°9. 小明早上骑自行车上学,中途因道路施工步行一段路,到学校共用20分钟,他骑自行车的平均速度是200米/分,步行的速度是70米/分,他家离学校的距离是3350米.设他骑自行车和步行的时间分别为x、y分钟,则列出的二元一次方程组是( ).A、 B、 C、 D、10. 如图,周董从A处出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,则∠ABC的度数是( )
A、30° B、36° C、45° D、72°9. 小明早上骑自行车上学,中途因道路施工步行一段路,到学校共用20分钟,他骑自行车的平均速度是200米/分,步行的速度是70米/分,他家离学校的距离是3350米.设他骑自行车和步行的时间分别为x、y分钟,则列出的二元一次方程组是( ).A、 B、 C、 D、10. 如图,周董从A处出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,则∠ABC的度数是( ) A、80° B、90° C、100° D、95°11. 若定义:f(a,b)=(﹣a,b),g(m,n)=(m,﹣n),例如f(1,2)=(﹣1,2),g(﹣4,﹣5)=(﹣4,5),则g(f(2,﹣3))=( )A、(2,﹣3) B、(﹣2,3) C、(2,3) D、(﹣2,﹣3)12. 已知直角坐标系中,点P(x,y)满足(5x+2y﹣12)2+|3x+2y﹣6|=0,则点P坐标为( )A、(3,﹣1.5) B、(﹣3,﹣1.5) C、(﹣2,﹣3) D、(2,﹣3)
A、80° B、90° C、100° D、95°11. 若定义:f(a,b)=(﹣a,b),g(m,n)=(m,﹣n),例如f(1,2)=(﹣1,2),g(﹣4,﹣5)=(﹣4,5),则g(f(2,﹣3))=( )A、(2,﹣3) B、(﹣2,3) C、(2,3) D、(﹣2,﹣3)12. 已知直角坐标系中,点P(x,y)满足(5x+2y﹣12)2+|3x+2y﹣6|=0,则点P坐标为( )A、(3,﹣1.5) B、(﹣3,﹣1.5) C、(﹣2,﹣3) D、(2,﹣3)二、填空题
-
13. 把命题“实数是无理数”改成“如果…,那么…”的形式; , 它是个命题.(填“真”或“假”)14. 如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠ABE=20°,那么∠EFC′的度数为度.
 15. 已知c的立方根为3,且(a﹣4)2+ =0,则a+6b+c的平方根是 .16. 如图,已知A1(1,0),A2(1,﹣1),A3(﹣1,﹣1),A4(﹣1,1),A5(2,1),…,则点A2010的坐标是 .
15. 已知c的立方根为3,且(a﹣4)2+ =0,则a+6b+c的平方根是 .16. 如图,已知A1(1,0),A2(1,﹣1),A3(﹣1,﹣1),A4(﹣1,1),A5(2,1),…,则点A2010的坐标是 .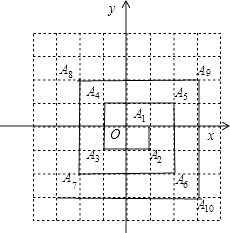
三、解答题
-
17. 计算:(1)、计算: + ﹣|1﹣ |;(2)、解方程组 .18. 填写推理理由:
如图,CD∥EF,∠1=∠2,求证:∠3=∠ACB.
证明:∵CD∥EF,
∴∠DCB=∠2
∵∠1=∠2,∴∠DCB=∠1.
∴GD∥CB .
∴∠3=∠ACB .
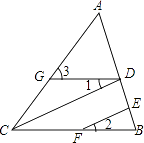 19. 已知△ABC三个顶点的坐标分别是 A(﹣3,﹣1)、B(1,3)、C(2,﹣3)
19. 已知△ABC三个顶点的坐标分别是 A(﹣3,﹣1)、B(1,3)、C(2,﹣3) (1)、在平面直角坐标系中描出各点并画出△ABC;(2)、将△ABC向下平移3个单位,再向右平移2个单位,得到△A′B′C′,画出△A′B′C;(3)、求△ABC的面积.20. 综合题。(1)、 = , = , = , = , = ,(2)、根据计算结果,回答: 一定等于a吗?你发现其中的规律了吗?请你把得到规律描述出来.(3)、利用你总结的规律,计算: .21. 已知关于x,y的二元一次方程组 的解适合方程x+y=6,求n的值.22. 阅读并补充下面推理过程:
(1)、在平面直角坐标系中描出各点并画出△ABC;(2)、将△ABC向下平移3个单位,再向右平移2个单位,得到△A′B′C′,画出△A′B′C;(3)、求△ABC的面积.20. 综合题。(1)、 = , = , = , = , = ,(2)、根据计算结果,回答: 一定等于a吗?你发现其中的规律了吗?请你把得到规律描述出来.(3)、利用你总结的规律,计算: .21. 已知关于x,y的二元一次方程组 的解适合方程x+y=6,求n的值.22. 阅读并补充下面推理过程: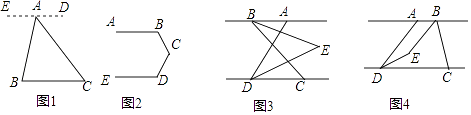 (1)、如图1,已知点A是BC外一点,连接AB,AC.求∠BAC+∠B+∠C的度数.
(1)、如图1,已知点A是BC外一点,连接AB,AC.求∠BAC+∠B+∠C的度数.解:过点A作ED∥BC,所以∠B= ,∠C= .
又因为∠EAB+∠BAC+∠DAC=180°.
所以∠B+∠BAC+∠C=180°.
(2)、如图2,已知AB∥ED,求∠B+∠BCD+∠D的度数.(3)、已知AB∥CD,点C在点D的右侧,∠ADC=70°,BE平分∠ABC,DE平分∠ADC,BE,DE所在的直线交于点E,点E在AB与CD两条平行线之间.Ⅰ.如图3,点B在点A的左侧,若∠ABC=60°,则∠BED的度数为 °.
Ⅱ.如图4,点B在点A的右侧,且AB<CD,AD<BC.若∠ABC=n°,则∠BED的度数为 °.(用含n的代数式表示)