新人教版数学九年级上册第二十二章第三节实际问题与二次函数
试卷更新日期:2016-01-13 类型:同步测试
一、选择题
-
1. 函数y=x2+2x-3(-2⩽x⩽2)的最大值和最小值分别是( )A、4和-3 B、-3和-4 C、5和-4 D、-1和-42. 如果一个实际问题的函数图象的形状与y= 的形状相同,且顶点坐标是(4,-2),那么它的函数解析式为( ).A、y=
 B、y=
B、y=  或y=
或y= 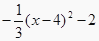 C、y=
D、y=
C、y=
D、y=  或y=
3. 一台机器原价100万元,每年的折旧率是x , 两年后这台机器约为y万元,则y与x的函数关系式为( )A、y=100(1-x)2 B、y=100(1-x) C、y=100-x2 D、y=100(1+x)24. 某商店经营皮鞋,所获利润y(元)与销售单价x(元)之间的关系为y=-x2+24x+2956,则获利最多为( ).A、3144 B、3100 C、144 D、29565. 童装专卖店销售一种童装,若这种童装每天获利y(元)与销售单价x(元)满足关系y=-x2+50x-500,则要想获得最大利润应定价为( ).A、25元 B、20元 C、30元 D、40元6. 苹果熟了,从树上落下所经过的路程s与下落的时间t满足 (g是不为0的常数),则s与t的函数图象大致是( )
或y=
3. 一台机器原价100万元,每年的折旧率是x , 两年后这台机器约为y万元,则y与x的函数关系式为( )A、y=100(1-x)2 B、y=100(1-x) C、y=100-x2 D、y=100(1+x)24. 某商店经营皮鞋,所获利润y(元)与销售单价x(元)之间的关系为y=-x2+24x+2956,则获利最多为( ).A、3144 B、3100 C、144 D、29565. 童装专卖店销售一种童装,若这种童装每天获利y(元)与销售单价x(元)满足关系y=-x2+50x-500,则要想获得最大利润应定价为( ).A、25元 B、20元 C、30元 D、40元6. 苹果熟了,从树上落下所经过的路程s与下落的时间t满足 (g是不为0的常数),则s与t的函数图象大致是( )
A、 B、
B、 C、
C、 D、
D、 7.
7.某幢建筑物,从10米高的窗口A用水管向外喷水,喷出的水流呈抛物线状(抛物线所在平面与墙面垂直,如图).若抛物线的最高点P离墙一米,离地面 米,则水流落地点B离墙的距离OB是( ).
 A、2米 B、3米 C、4米 D、5米8. 长为20cm , 宽为10cm的矩形,四个角上剪去边长为xcm的小正方形,然后把四边折起来,作成底面为ycm2的无盖的长方体盒子,则y与x的关系式为( ).A、y=(10-x)(20-x)(0 x 5) B、y=10×20-4x2(0 x 5) C、y=(10-2x)(20-2x)(0 x 5) D、y=200+4x2(0 x 5)9. 某大学的校门是一抛物线形水泥建筑物(如图所示),大门的地面宽度为8米,两侧距地面4米高处各有一个挂校名匾用的铁环,两铁环的水平距离为6米,则校门的高约为( )(精确到0.1米,水泥建筑物的厚度忽略不记).
A、2米 B、3米 C、4米 D、5米8. 长为20cm , 宽为10cm的矩形,四个角上剪去边长为xcm的小正方形,然后把四边折起来,作成底面为ycm2的无盖的长方体盒子,则y与x的关系式为( ).A、y=(10-x)(20-x)(0 x 5) B、y=10×20-4x2(0 x 5) C、y=(10-2x)(20-2x)(0 x 5) D、y=200+4x2(0 x 5)9. 某大学的校门是一抛物线形水泥建筑物(如图所示),大门的地面宽度为8米,两侧距地面4米高处各有一个挂校名匾用的铁环,两铁环的水平距离为6米,则校门的高约为( )(精确到0.1米,水泥建筑物的厚度忽略不记).
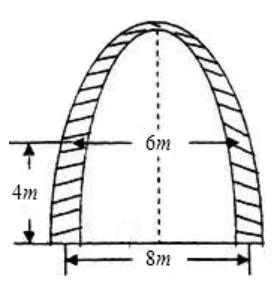
A、5.1米 B、9米 C、9.1米 D、9.2米10. 有一拱桥的桥拱是抛物线形, 其表达式是Y=-0.25x2 , 当桥下水面宽为12米时,水面到拱桥拱顶的距离为( )A、3米 B、2 米 C、4 米 D、9米二、填空题
-
11. 如图所示是一学生推铅球时,铅球行进高度y(m)与水平距离x(m)的函数图象.现观察图象,铅球推出的距离是m .
 12. 用长度一定的绳子围成一个矩形,如果矩形的一边长x(m)与面积y(m2)满足函数关系y=-(x-12)2+144(0<x<24),那么该矩形面积的最大值为m2 .13. 某物体从上午7时至下午4时的温度M(℃)是时间t(h)的函数:M=t2-5t+100(其中t=0表示中午12时,t=1表示下午1时),则上午10时此物体的温度为℃.14.
12. 用长度一定的绳子围成一个矩形,如果矩形的一边长x(m)与面积y(m2)满足函数关系y=-(x-12)2+144(0<x<24),那么该矩形面积的最大值为m2 .13. 某物体从上午7时至下午4时的温度M(℃)是时间t(h)的函数:M=t2-5t+100(其中t=0表示中午12时,t=1表示下午1时),则上午10时此物体的温度为℃.14.用铝合金型材做一个形状如图(1)所示的矩形窗框,设窗框的一边为xm , 窗户的透光面积为ym2 , y与x的函数图象如图(2)所示.观察图象,当x=时,窗户透光面积最大.
 15.
15.隧道的截面是抛物线,且抛物线的解析式为y=—
 ,一辆车高3m , 宽4m , 该车通过该隧道.(填“能”或“不能”)16. 两个数的和为6,这两个数的积最大可以达到 .17.
,一辆车高3m , 宽4m , 该车通过该隧道.(填“能”或“不能”)16. 两个数的和为6,这两个数的积最大可以达到 .17.如下图是抛物线 和一次函数
 的图象,观察图象写出
的图象,观察图象写出  时,
时,  的取值范围.
的取值范围. 18. 如图,用一段长为30米的篱笆围成一个一边靠墙(墙的长度不限)的矩形
18. 如图,用一段长为30米的篱笆围成一个一边靠墙(墙的长度不限)的矩形
菜园 ,设 边长为
,设 边长为  米,则菜园的面积
米,则菜园的面积  (单位:米 )与
(单位:米 )与
 (单位:米)的函数关系式为(不要求写出自变量
(单位:米)的函数关系式为(不要求写出自变量  的取值范围). 19. 某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加利润,尽快减少库存,商场决定采取适当的降价措施.经调查发现:如果每件衬衫降价1元,商场平均每天可多售出2件.则商场降价后每天盈利y(元)与降价x(元)的函数关系式为 .
的取值范围). 19. 某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加利润,尽快减少库存,商场决定采取适当的降价措施.经调查发现:如果每件衬衫降价1元,商场平均每天可多售出2件.则商场降价后每天盈利y(元)与降价x(元)的函数关系式为 .三、解答题
-
20.
如图,八一广场要设计一个矩形花坛,花坛的长、宽分别为200m、120m,花坛中有一横两纵的通道,横、纵通道的宽度分别为3xm、2xm.
 (1)、
(1)、用代数式表示三条通道的总面积S;当通道总面积为花坛总面积的
 时,求横、纵通道的宽分别是多少?(2)、如果花坛绿化造价为每平方米3元,通道总造价为3168x元,那么横、纵通道的宽分别为多少米时,花坛总造价最低?并求出最低造价.(以下数据可供参考:852=7225,862=7396,872=7569)21.
时,求横、纵通道的宽分别是多少?(2)、如果花坛绿化造价为每平方米3元,通道总造价为3168x元,那么横、纵通道的宽分别为多少米时,花坛总造价最低?并求出最低造价.(以下数据可供参考:852=7225,862=7396,872=7569)21.如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A,D不重合).BE的垂直平分线交AB于M,交DC于N.
 (1)、设AE=x,四边形ADNM的面积为S,写出S关于x的函数关系式;(2)、当AE为何值时,四边形ADNM的面积最大?最大值是多少?22.
(1)、设AE=x,四边形ADNM的面积为S,写出S关于x的函数关系式;(2)、当AE为何值时,四边形ADNM的面积最大?最大值是多少?22.某公司试销一种成本为30元/件的新产品,按规定试销时的销售单价不低于成本单价,又不高于80元/件,试销中每天的销售量y(件)与销售单价x(元/件)满足下表中的函数关系.
 (1)、试求y与x之间的函数表达式;(2)设公司试销该产品每天获得的毛利润为S(元),求S与x之间的函数表达式(毛利润=销售总价-成本总价);(2)、当销售单价定为多少时,该公司试销这种产品每天获得的毛利润最大?(3)、最大毛利润是多少?此时每天的销售量是多少?23. 杭州休博会期间,嘉年华游乐场投资150万元引进一项大型游乐设施.若不计维修保养费用,预计开放后每月可创收33万元.而该游乐设施开放后,从第1个月到第x个月的维修保养费用累计为y(万元),且y=ax2+bx;若将创收扣除投资和维修保养费用称为游乐场的纯收益g(万元),g也是关于x的二次函数;(1)、若维修保养费用第1个月为2万元,第2个月为4万元.求y关于x的解析式;(2)、求纯收益g关于x的解析式;(3)、问设施开放几个月后,游乐场的纯收益达到最大;几个月后,能收回投资?24. 有一种葡萄:从树上摘下后不保鲜最多只能存放一周,如果放在冷藏室,可以延长保鲜时间,但每天仍有一定数量的葡萄变质,假设保鲜期内的重量基本保持不变,现有一位个体户,按市场价收购了这种葡萄200千克放在冷藏室内,此时市场价为每千克2元,据测算,此后每千克鲜葡萄的市场价格每天可以上涨0.2元,但是,存放一天需各种费用20元,平均每天还有1千克葡萄变质丢弃.(1)、设x天后每千克鲜葡萄的市场价为P元,写出P关于x的函数关系式;
(1)、试求y与x之间的函数表达式;(2)设公司试销该产品每天获得的毛利润为S(元),求S与x之间的函数表达式(毛利润=销售总价-成本总价);(2)、当销售单价定为多少时,该公司试销这种产品每天获得的毛利润最大?(3)、最大毛利润是多少?此时每天的销售量是多少?23. 杭州休博会期间,嘉年华游乐场投资150万元引进一项大型游乐设施.若不计维修保养费用,预计开放后每月可创收33万元.而该游乐设施开放后,从第1个月到第x个月的维修保养费用累计为y(万元),且y=ax2+bx;若将创收扣除投资和维修保养费用称为游乐场的纯收益g(万元),g也是关于x的二次函数;(1)、若维修保养费用第1个月为2万元,第2个月为4万元.求y关于x的解析式;(2)、求纯收益g关于x的解析式;(3)、问设施开放几个月后,游乐场的纯收益达到最大;几个月后,能收回投资?24. 有一种葡萄:从树上摘下后不保鲜最多只能存放一周,如果放在冷藏室,可以延长保鲜时间,但每天仍有一定数量的葡萄变质,假设保鲜期内的重量基本保持不变,现有一位个体户,按市场价收购了这种葡萄200千克放在冷藏室内,此时市场价为每千克2元,据测算,此后每千克鲜葡萄的市场价格每天可以上涨0.2元,但是,存放一天需各种费用20元,平均每天还有1千克葡萄变质丢弃.(1)、设x天后每千克鲜葡萄的市场价为P元,写出P关于x的函数关系式;
(2)、若存放x天后将鲜葡萄一次性出售,设鲜葡萄的销售金额为y元,写出y关于x的函数关系式;(3)、问个体户将这批葡萄存放多少天后出售,可获得最大利润,最大利润q是多少?