初中数学浙教版八年级上册3.2 不等式的基本性质 强化提升训练
试卷更新日期:2019-09-20 类型:同步测试
一、中考演练
-
1. 实数a、b、c满足a>b且ac<bc,它们在数轴上的对应点的位置可以是( )A、
 B、
B、 C、
C、 D、
D、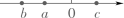 2. 设0< <1,则m= ,则m的取值范围是.3. 用一组 , , 的值说明命题“若 ,则 ”是错误的,这组值可以是 , , .
2. 设0< <1,则m= ,则m的取值范围是.3. 用一组 , , 的值说明命题“若 ,则 ”是错误的,这组值可以是 , , .二、综合提升
-
4. 有数颗等重的糖果和数个大、小砝码,其中大砝码皆为5克、小砝码皆为1克,如图是将糖果与砝码放在等臂天平上的两种情形。判断下列选项中哪一种情形是正确的( )
 A、
A、 B、
B、 C、
C、 D、
D、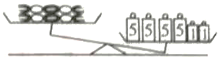 5. 已知0≤a﹣b≤1且1≤a+b≤4,则a的取值范围是( )A、1≤a≤2 B、2≤a≤3 C、 ≤a≤ D、 ≤a≤6. 若a>b,则下列各式中一定成立的是( )A、ma>mb B、c2a>c2b C、(1+c2)a>(1+c2)b D、1﹣a>1﹣b7. 某运行程序如图所示,规定:从“输入一个值x到结果是否>95”为一次程序操作,如果程序操作进行了二次才停止,那么x的取值范围是( )
5. 已知0≤a﹣b≤1且1≤a+b≤4,则a的取值范围是( )A、1≤a≤2 B、2≤a≤3 C、 ≤a≤ D、 ≤a≤6. 若a>b,则下列各式中一定成立的是( )A、ma>mb B、c2a>c2b C、(1+c2)a>(1+c2)b D、1﹣a>1﹣b7. 某运行程序如图所示,规定:从“输入一个值x到结果是否>95”为一次程序操作,如果程序操作进行了二次才停止,那么x的取值范围是( ) A、x>23 B、x≤47 C、23≤x<47 D、23<x≤478. 下列结论不正确的是( ).A、若a-5<b-5,则a<b. B、若a>b,c>d,则a+c>b+d. C、若2a>-2b,则a>-b. D、若x2>1,则x>9. 5名学生身高两两不同,把他们按从高到低排列,设前三名的平均身高为a米,后两名的平均身高为b米.又前两名的平均身高为c米,后三名的平均身高为d米,则( )A、 >
A、x>23 B、x≤47 C、23≤x<47 D、23<x≤478. 下列结论不正确的是( ).A、若a-5<b-5,则a<b. B、若a>b,c>d,则a+c>b+d. C、若2a>-2b,则a>-b. D、若x2>1,则x>9. 5名学生身高两两不同,把他们按从高到低排列,设前三名的平均身高为a米,后两名的平均身高为b米.又前两名的平均身高为c米,后三名的平均身高为d米,则( )A、 >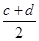 B、
B、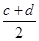 >
C、
>
C、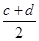 =
D、以上都不对
10. 若关于 的不等式 的解集为 ,化简 .11. 下边的框图表示解不等式3-5x>4-2x 的流程,其中“系数化为 1”这一步骤的依据是 .
=
D、以上都不对
10. 若关于 的不等式 的解集为 ,化简 .11. 下边的框图表示解不等式3-5x>4-2x 的流程,其中“系数化为 1”这一步骤的依据是 .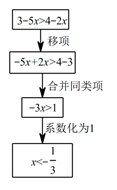 12. 已知a<0,-1<b<0,试比较a、ab、ab2的大小.13. 【提出问题】已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围.
12. 已知a<0,-1<b<0,试比较a、ab、ab2的大小.13. 【提出问题】已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围.【分析问题】先根据已知条件用一个量如取y表示另一个量如x,然后根据题中已知量x的取值范围,构建另一个量y的不等式,从而确定该量y的取值范围,同法再确定另一未知量x的取值范围,最后利用不等式性质即可获解.
【解决问题】解:∵x﹣y=2,∴x=y+2.
又∵x>1,∴y+2>1,∴y>﹣1.
又∵y<0,∴﹣1<y<0,…①
同理得1<x<2…②
由①+②得﹣1+1<y+x<0+2.
∴x+y的取值范围是0<x+y<2.
【尝试应用】已知x﹣y=﹣3,且x<﹣1,y>1,求x+y的取值范围.