人教版初中数学九年级上册第二十一章一元二次方程21.2.1配方法 同步训练
试卷更新日期:2016-01-12 类型:同步测试
一、选择题
-
1. 方程 左边配成一个完全平方公式后,所得的方程是( )A、 B、 C、 D、2. 下列方程能用直接开平方法解的是( )A、
 B、
B、 C、
D、
3.
C、
D、
3.用直接开平方法解方程
 ,方程的根为( )A、 B、 C、
,方程的根为( )A、 B、 C、 D、
D、 4.
4.方程 的根为( )
A、2 B、-2 C、±2 D、无实根5.一元二次方程
 可转化为两个一元一次方程,其中一个一元一次方程是 ,则另一个一元一次方程是( ).A、
可转化为两个一元一次方程,其中一个一元一次方程是 ,则另一个一元一次方程是( ).A、 B、
C、
D、
6.
B、
C、
D、
6.方程
 的实数根的个数是( )A、0 B、1 C、2 D、37.
的实数根的个数是( )A、0 B、1 C、2 D、37.方程 整理成一般形式后为( )
A、 B、
B、 C、
C、 D、
8. 已知方程 可以配方成
D、
8. 已知方程 可以配方成 的形式,那么 的值是( ) A、-2 B、-1 C、1 D、29.
的形式,那么 的值是( ) A、-2 B、-1 C、1 D、29.把一元二次方程 化成 的形式,则 的值( )
A、3 B、5 C、6 D、810. 如果x2+2(1-2m)x+9=0(m≠0)的左边是一个关于x的完全平方公式,则m等于( ).A、1 B、-1 C、-1或1 D、-1或211.已知
 ,则 等于( )A、1 B、-1 C、 D、-12. 已知b<0,关于x的一元二次方程(x﹣1)2=b的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、有两个实数根13. 将二次三项式x2-4x+1配方后得( ).A、(x-2)2+3 B、(x-2)2-3 C、(x+2)2+3 D、(x+2)2-314.
,则 等于( )A、1 B、-1 C、 D、-12. 已知b<0,关于x的一元二次方程(x﹣1)2=b的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、有两个实数根13. 将二次三项式x2-4x+1配方后得( ).A、(x-2)2+3 B、(x-2)2-3 C、(x+2)2+3 D、(x+2)2-314.三角形两边的长是3和4,第三边的长是方程 的根,则该三角形的周长为( ).
A、14 B、12 C、12或14 D、以上都不对15.如图,在平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程 的根,则平行四边形ABCD的周长为( )
 A、 B、 C、 D、
A、 B、 C、 D、
二、填空题
-
16. =( +)2; =( -)217.
①方程
 的根是;②方程 的根是.18. 若关于x的一元二次方程 有实数根,则n的取值范围是.19. 如果二次三项式 是一个完全平方式,那么 m 的值是.
的根是;②方程 的根是.18. 若关于x的一元二次方程 有实数根,则n的取值范围是.19. 如果二次三项式 是一个完全平方式,那么 m 的值是.
20.代数式
 有最值,最值是.
有最值,最值是.三、解答题
-
21. 解下列方程:(1)、
 (2)、y2-2y-3=0(3)、
(2)、y2-2y-3=0(3)、 22.
22.试用配方法证明:代数式 的值不小于3.
 的值.
的值. ,则 ,原方程化为 ①
,则 ,原方程化为 ① 原方程的解为
原方程的解为 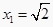 , , ,
, , ,  .
.