初中数学浙教版七年级上册第三章 实数 章末检测
试卷更新日期:2019-09-20 类型:单元试卷
一、单选题
-
1. 下列说法:
( 1 )任何数都有算术平方根;(2)一个数的算术平方根一定是正数;(3)a的算术平方根是a;(4)( -4)2的算术平方根是 -4;(5)算术平方根不可能是负数.其中不正确的有( )
A、5个 B、4个 C、3个 D、2个2. 如图,A,B,C,D是数轴上的四个点,其中最适合表示无理数 的点是( )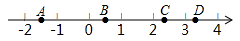 A、点A B、点B C、点C D、点D3. 点 在数轴上的位置如图所示, 为原点, , .若点 所表示的数为 ,则点 所表示的数为( )
A、点A B、点B C、点C D、点D3. 点 在数轴上的位置如图所示, 为原点, , .若点 所表示的数为 ,则点 所表示的数为( )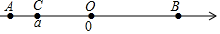 A、 B、 C、 D、4. 以下各数中, 、﹣2、0、3 、 、﹣1.732、 、 、3+ 、0.1010010001…中无理数的个数有( )A、1个 B、2个 C、3个 D、4个5. 下列说法正确的是( )A、不是有限小数就是无理数 B、带根号的数都是无理数 C、无理数一定是无限小数 D、所有无限小数都是无理数6. 下列说法中,不正确的是( )A、10的立方根是 B、-2是4的一个平方根 C、 的平方根是 D、0.01的算术平方根是0.17. 下列说法中错误的是( )A、 中的 可以是正数、负数或零 B、 中的 不可能是负数 C、数 的平方根有两个 D、数 的立方根有一个8. 下列整数中,与 最接近的是( )A、4 B、5 C、6 D、79. 把5的平方根和立方根按从小到大的顺序排列为( )A、 B、 C、 D、10. 在期末复习课上,老师要求写出几个与实数有关的结论:小明同学写了以下5个:
A、 B、 C、 D、4. 以下各数中, 、﹣2、0、3 、 、﹣1.732、 、 、3+ 、0.1010010001…中无理数的个数有( )A、1个 B、2个 C、3个 D、4个5. 下列说法正确的是( )A、不是有限小数就是无理数 B、带根号的数都是无理数 C、无理数一定是无限小数 D、所有无限小数都是无理数6. 下列说法中,不正确的是( )A、10的立方根是 B、-2是4的一个平方根 C、 的平方根是 D、0.01的算术平方根是0.17. 下列说法中错误的是( )A、 中的 可以是正数、负数或零 B、 中的 不可能是负数 C、数 的平方根有两个 D、数 的立方根有一个8. 下列整数中,与 最接近的是( )A、4 B、5 C、6 D、79. 把5的平方根和立方根按从小到大的顺序排列为( )A、 B、 C、 D、10. 在期末复习课上,老师要求写出几个与实数有关的结论:小明同学写了以下5个:①任何无理数都是无限不循环小数;②有理数与数轴上的点一一对应;③在1和3之间的无理数有且只有 这4个;④ 是分数,它是有理数;⑤由四舍五入得到的近似数7.30表示大于或等于7.295,而小于7.305的数.
其中正确的个数是( )
A、1 B、2 C、3 D、4二、填空题
-
11. 已知: , , , , , ,3.1415926,-1, , ,0.2020020002…(相邻两个2之间0的个数逐次加1)其中无理数有个.12. 已知实数a、b都是比2小的数,其中a是整数,b是无理数,请根据要求,分别写出一个a、b的值:a= , b= .13. 若一个数的立方根等于这个数的算术平方根,则这个数是.14. 已知a,b为两个连续整数,且a< <b,则a+b的值为 .15. 若某个正数的平方根是a﹣3和a+5,则这个正数是 .16. 利用上面的规律,比较 的大小.(填“>”或“<”).
三、解答题
-
17. 把下列各数填在相应的括号内:
整数:
分数:
无理数:
实数:
18. 把下列各数的序号填在相应的大括号内:①﹣17;②π;③﹣|﹣ |;④ ;⑤ ;⑥﹣0.92;⑦ ;⑧﹣0. ;⑨1.2020020002;
(1)、正实数{ }负有理数{ }
无理数{ }
(2)、从以上9个数中选取2个有理数,2个无理数,用“+、﹣、×、÷”中的3种不同的运算符号将选出的4个数进行运算(可以用括号),使得计算结果为正整数,列出式子并计算.19. 计算(1)、 ;(2)、20. 在数轴上近似表示出数 ,并把它们从小到大用“<”连接起来。 21. 已知x﹣2的平方根是±2,5y+32的立方根是﹣2.
21. 已知x﹣2的平方根是±2,5y+32的立方根是﹣2.
(1)、求x3+y3的平方根.
(2)、计算:|2﹣ |- 的值.22. 已知5a+2的立方根是3,3a+b-1的算术平方根是4,c是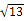 的整数部分. (1)、求a,b,c的值;(2)、求3a-b+c的平方根23. 讲解完本节,王老师在小结时总结了这样一句话:“对于任意两个整数a、b,如果a>b,那么 > .”然后讲了下面的一个例题:比较 和 的大小.
的整数部分. (1)、求a,b,c的值;(2)、求3a-b+c的平方根23. 讲解完本节,王老师在小结时总结了这样一句话:“对于任意两个整数a、b,如果a>b,那么 > .”然后讲了下面的一个例题:比较 和 的大小.方法一: = = , = = ,
又∵8<12,
∴ < .
方法二: = ×200=8, =4×3=12.
又∵8<12,
∴ < .
根据上面的例题解答下列各题:
(1)、比较 和 的大小;(2)、比较 ﹣1与 ﹣ 的大小.24. 阅读下面的文字,解答问题大家知道, 是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部地写出来,于是小明用 ﹣1来表示 的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理的,因为 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如因为 < < ,即2< <3,所以行的整数部分为2,小数部分为 ﹣2.
请解答
(1)、 的整数部分为;小数部分为;(2)、有人说,如果 的整数部分为x, 的小数部分记为y,则x+y= ,你认为对吗?为什么?(3)、如果 的整数部分为a, 的小数部分为b,求a﹣2b+2 的值.